Über Parkettierungen

Als Parkettierung bezeichnet man die lückenlose Auslegung einer Ebene mit Fliesen. Sind diese gleich geformt, gleich groß und außerdem regelmäßige Polygone, gibt es nur drei Möglichkeiten: Quadrate, Dreiecke und Sechsecke.

Läßt man die Forderung nach Regelmäßigkeit fallen, kommen auch Rechtecke, ja beliebig geformte Vielecke in Betracht. Auch krummlinig begrenzte Fliesen eignen sich unter Umständen zur Parkettierung. Berühmte Beispiele hierfür stammen von M. C. Escher [1a],[1b]. Bei dem zweiten wird zugelassen, daß die verwendeten Fliesen umgedreht werden, so daß ihre Unterseite nach oben kommt. Es stellt einen Reiter zu Pferde dar, der sich mit seinem Spiegelbild periodisch wiederholt und mit ihm ohne Zwischenräume verzahnt ist. (Über Parkettierungen mit unregelmäßigen Vielecken und daraus gewonnene, krummlinige Figuren siehe z. B. in [2].)

Werden Fliesen unterschiedlicher Form oder Größe verwendet, gelingt die Parkettierung häufig nicht mehr. Dies ist nur dann der Fall, wenn sie in ihrer Art so gewählt wurden, daß sie zueinander passen. Häufig sind dabei mehrere Fliesensorten zugleich in Gebrauch. Eine Frage, die hierbei gestellt werden kann, lautet: mit wie wenig verschiedenen Fliesenarten kommt man beim Parkettieren aus, und welche Form haben die betreffenden Fliesen? Die Antwort ist: es genügen zwei unterschiedliche Arten, wobei die Fliesen jeweils einer Sorte unter sich gleich groß sind. Ein einfaches Beispiel (ohne den Rand) verwendet Achteck und Quadrat:



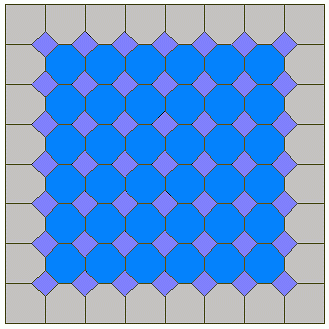
Dabei handelt es sich um ein Muster, das ähnlich an der Fassade einer italienischen Kirche aus dem 15. Jhdt. zu sehen war [3]



und vermutlich noch sehr viel älter ist.

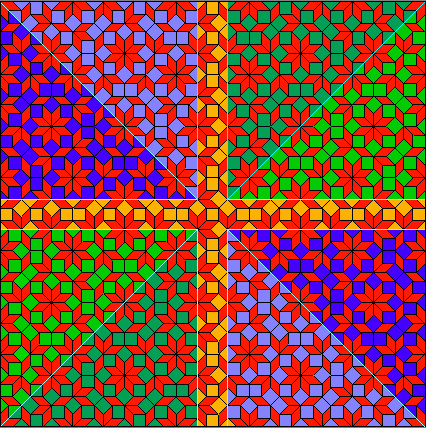
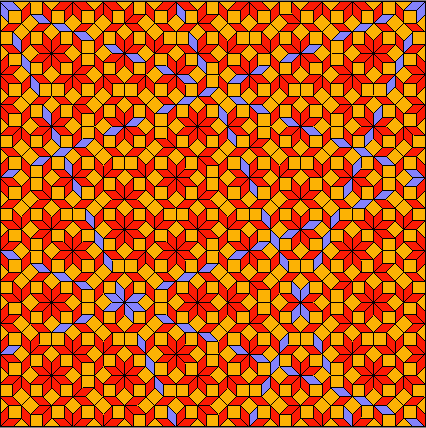
Erst aus den 70er Jahren des vorigen Jahrhunderts stammt das folgende Parkett von Roger Penrose [4]:

 Fig. A

Es besteht aus zwei Rauten, einer breiten mit einem 72-Grad-Winkel an den Spitzen und einer schmalen mit 36 Grad. Die Seiten der beiden Rauten sind gleich lang.

Ein weiteres Parkett wurde von Robert Ammann und Frans P. M. Beenker entdeckt. Grundformen dabei sind eine Raute und ein Quadrat [5]:

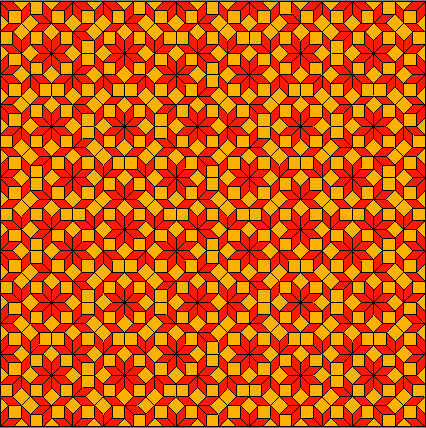 Fig. B

Im Gegensatz zu dem Achteck-Quadrat-Parkett und anderen periodischen Mustern sind Penrose-Parkette unperiodisch. Das heißt: bestimmte Details wiederholen sich zwar ständig, aber dies geschieht nicht regelmäßig. Es gibt dafür kein klares, leicht erkennbares Schema.

Trotzdem ist es, zumindest bei dem obigen Beispiel (Fig. A), bis zu einem gewissen Grade möglich, sich während des Verlegens an bereits fertigen Parkettbereichen zu orientieren und dort "abzugucken". Dies wird deutlich, wenn man das Bild um 90 Grad dreht und seine Fliesen zum Teil anders färbt:

 (ursprünglich)

 (gedreht)



Die hier sichtbar werdenden Achsensymmetrien erleichtern das Verlegen des Parketts, und sie sind nicht die einzigen.

Bei weiteren Bereichen mit schräg verlaufenden Symmetrieachsen deuten ihre Umrisse die beiden Penrose-Rauten an:

 

Das Ammann-Beenker-Parkett ist ebenfalls unperiodisch mit denselben Schwierigkeiten beim Verlegen, doch gibt es auch hier bei dem angeführten Beispiel (Fig. B) Regelmäßigkeiten, die durch Umfärben sichtbar gemacht werden können:



Die mehr kuriositätshalber ausgewählte obere Form läßt sich durch einfaches Verschieben reproduzieren. Nützlich für die Erstellung eines Verlegungsplanes, etwa beim Pflastern eines Grundstückes, sind auch bei Fig. B achsensymmetrische Teile:



Etwas ungleichmäßig wirkt der kreuzförmige Mittelteil, doch verschwindet dieser Eindruck, wenn man die Figur um 45 Grad nach links verdreht. Dann ist besser zu erkennen, daß die beiden Kreuzhälften, getrennt durch eine (unterbrochene) lotrechte Linie, ebenfalls spiegelsymmetrisch zueinander liegen. Die gesamte Figur ist symmetrisch zur Winkelhalbierenden des ersten und dritten Quadranten; dies fällt bei der Originalfärbung nicht sofort ins Auge.

Anmerkung.: Beim Betrachten der Fig. B mit leicht zusammengekniffenen Augen vermeint man, schräg verlaufende gerade Linien zu sehen. Einige von ihnen sind in der folgenden Figur farblich hervorgehoben. Ob sie eine tiefere Bedeutung haben, scheint nicht bekannt zu sein. (Zum Teil, streckenweise und über nicht zu große beiderseitige Entfernungen sind es Symmetrieachsen.)

*

Abschließend ein angefangenes eigenes Parkett aus gleichseitigen Dreiecken und Rauten, das ebenfalls unperiodisch ist:

*

Ergänzung: Regelmäßige Muster wie die folgenden erinnern eher an feine Häkel- und Spitzenarbeiten als an Parkette für Fußböden und Wände, und die Frage lautet: Wie entstehen sie?

 
 

Nun noch ganz zum Schluß ein regelmäßiges, etwas irritierendes Parkett:



die durchgehenden blauen Strecken sind parallel. Der gegenteilige Eindruck ist eine optische Täuschung.

Lebende "Parkette"

Literatur:

[1a] http://www.mathe.tu-freiberg.de/~hebisch/cafe/mce/symm105.html
[1b] http://www.mathe.tu-freiberg.de/~hebisch/cafe/mce/symm67.html . Weiteres bei google,
        Suchwort: M. C. Escher.
[2]   http://geometrie.diefenbach.at
[3]   S. Sebastiano, Mantua (Restaurierungsvorschlag), F.A.Z. vom 19.3.02
[4]   http://tams-www.informatik.uni-hamburg.de/people/hendrich/penrose/penrose.html
[5]   www.itap.physik.uni-stuttgart.de/~gaehler/tilings/oct.html
[6]   Eine weitere Seite über nichtperiodische Parkette:
        www.mathematik.uni-bielefeld.de/baake/frettloe/bilder.html. Dort wird auch auf
[7]   http://jcrystal.com/steffenweber/JAVA/jtiling/jtiling.html, Seite mit einem JAVA-Applet
        zur automatischen Erzeugung rotationssymmetrischer, quasi-rhomboedrischer Parkette.

Nachtrag:
Ein dreidimensionales Analogon zu den zweidimensionalen, nichtperiodischen Penrose-Parketten bilden die Quasi-Kristalle von Daniel Shechtman.
Für ihre Entdeckung erhielt er nach anfänglichen Widerständen aus der Fachwelt 2011 den Nobelpreis für Chemie.
Näheres dazu z. B. hier, hier und hier (YouTube-Video mit Prof. Shechtman).

Zurück zu Geometrische Figuren
Zurück zur Hauptseite