Aus einem Zahnrad entstehende Phantasiekurven
Mit dem fedgeo lassen sich bequem die Graphen vieler Funktionen und Relationen zeichnen, wenn diese in der expliziten Form y=f(x) oder als Parameterdarstellung gegeben sind. Manche, wie Kegelschnitte, Spiralen und Lissajousfiguren, haben besondere Namen; die meisten sind namenlos.
In einem früheren Beitrag bildeten Zykloiden den Ausgangspunkt; im vorliegenden soll es die Figur eines Zahnrades mit abgerundeten Zähnen sein:

Sie entsteht, wenn ein Punkt P einen festen Punkt M umkreist, wobei der Abstand von diesem mit einer höheren Frequenz als der Umlauffrequenz periodisch um einen kleinen Betrag zu- und abnimmt. Demgemäß läßt sich ansetzen:


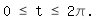
a>0 ist der mittlere Radius des Zahnrades; b, ebenfalls positiv, aber klein gegen a, bestimmt die Größe der Zähne, und n ist ihre Anzahl.
Von dieser Grundform ausgehend, kann man nun zu verschiedenen anderen Kurven gelangen, bei denen bald nichts mehr an ihre Herkunft erinnert.
Als erstes setze ich a=0, mache b größer als 1 (im folgenden Beispiel gleich 5) und reduziere die Anzahl n der Zähne auf 6. Dann entsteht eine Figur mit 12 Flügeln:
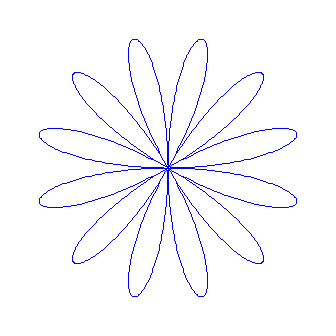
Soll eine gleich große Figur mit einer ungeraden Anzahl von Flügeln, beispielsweise 7, gezeichnet werden, wählen wir n=7, lassen aber den Parameter t nur noch im Bereich 0 bis Pi variieren:
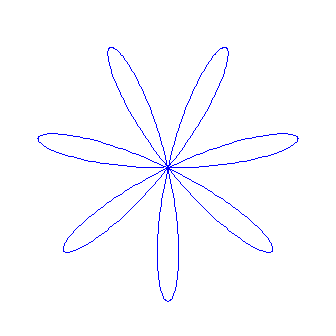
Nun wählen wir a wieder größer als Null und machen b erneut kleiner als 1, aber nicht so klein wie beim Zahnrad. Außerdem soll t wie dort wieder von 0 bis 2*Pi gehen:

Wird b weiter vergrößert, bleibt aber kleiner als a, ergibt sich z. B.

und wenn b deutlich größer als a wird, entstehen Schleifen auch im Innern der Figur:
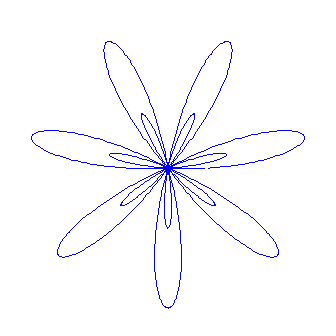
Dies alles läßt sich verhältnismäßig leicht voraussagen. Was aber passiert, wenn wir n nicht mehr als natürliche Zahl wählen wie beim Zahnrad und den Flügelfiguren? Mit n=3,5 statt bisher 7 und b=a ergibt sich beispielsweise:
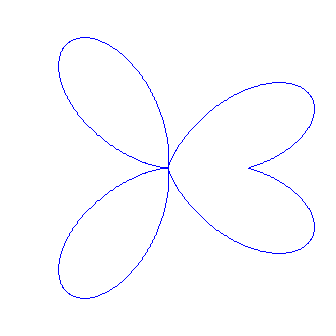
während man für n=3/4 erhält:

Was kann noch verändert werden? Eine Möglichkeit besteht darin, daß wir anstelle eines Wertes für n zwei verschiedene verwenden: n1 und n2, das eine bei x, das andere für y.
Entsprechend mit a und b: jeweils zwei verschiedene Zahlen a1 und a2, b1 und b2 werden ausgewählt, ganzzahlig oder gebrochen, positiv, Null oder negativ. Dazu kann man noch sin und cos miteinander vertauschen oder höhere Potenzen von ihnen verwenden - der Phantasie sind keine Grenzen gesetzt.
So entsteht z. B. diese Figur, die an einen Fisch erinnert:

Abschließend noch ein paar ergänzende Bemerkungen.
Rebecca hat mit dem fedgeo an anderer Stelle des Matheplaneten ein Zahnrad mit eckigen Zähnen gezeichnet und dazu auch von der hyperbolischen Tangensfunktion Gebrauch gemacht. Mit ihr habe ich ebenfalls ein wenig experimentiert und bin dabei auf das folgende Quadrat

gestoßen. Ohne tanh, nur mit sin und cos, entstehen lediglich "Quadrate" mit abgerundeten Ecken wie zum Beispiel dieses:
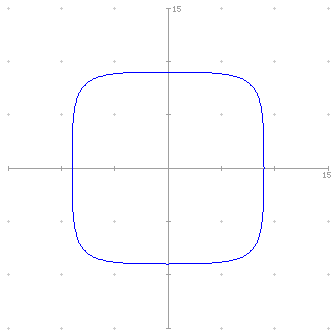
Hans-Jürgen
1)Anm.: Auf dem Matheplaneten selbst kann man durch Anklicken für jede Figur auch den fedgeo-Code sehen, was hier in der Offline-Darstellung (bis auf diese Ausnahme) nicht möglich ist.
|
Re:
Aus einem Zahnrad entstehende Phantasiekurven |
|
|
Zurück zur Themenübersicht