Gesucht sind alle Paare (x;y) natürlicher Zahlen x, y, für die gilt: xy = yx, x≠y.
Dies ist eine alte Aufgabe aus dem 18. Jahrhundert * , die hier auf dem Matheplaneten erneut gestellt wurde.
Bedingung war, dass nur Mittel verwendet werden, über die Schüler der 9. Klasse verfügen, d. h. keine Logarithmen (und keine Differentialrechnung, von der in den anschließenden Diskussionsbeiträgen teilweise die Rede war).
Zahlenpaare (x;y) mit gleichem x und y heißen "trivial" und sind uninteressant. Das kleinste nicht-triviale Paar (2;4) mit dem wegen der Symmetrie in x und y zugehörigen Paar (4;2) findet man am einfachsten durch Raten. Ob es noch mehr nicht-triviale gibt, war zu untersuchen.
Sei y=x+k, k∈ℕ, dann gilt: xx+k = (x+k)x und weiter
Wenn x und k natürliche Zahlen sein sollen, ist die linke Seite xk eine natürliche Zahl. Damit dies auch für die rechte gilt, muss auch der Inhalt der Klammer natürlich sein: 1+k/x= m∈ℕ. Damit wird
k=(m-1)x, was, eingsetzt in (1), auf x(m-1)x=mx und xm-1=m führt.
Für m=1 erhält man x0=1, k=0, y=1, was uninteressant ist, und für m=2: x1=x=2. Damit wird k=2 und y=x+k=4, d. h. wir haben das geratene, kleinste nicht-triviale Paar (2;4) und sein Pendant (4;2).
Für m=3,4,5,... ergeben sich mit xm-1=m für x die Zahlen
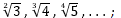 somit gibt es kein weiteres nicht-triviales Lösungspaar.
somit gibt es kein weiteres nicht-triviales Lösungspaar.
Zurück zur Übersichtsseite, Teil 1