1 + 2 + 3 + 4 + 5 + 6 + ... = ?
Eine unendliche Reihe hat die Form
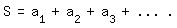
Dabei deutet S an, dass es sich um eine Summe handeln soll, und die Punkte sind als "und so weiter" zu lesen.
Die ai , i ∈ ℕ, sind feste reelle Zahlen oder hängen von einer, z. B. x genannten, Variablen ab. Beispiele:
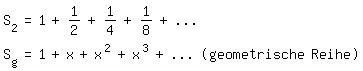
Eine Summe mit unendlich vielen Summanden (wie es die Punkte andeuten) kann man nicht berechnen, immer nur eine mit endlich vielen. Man bildet deshalb aus den ersten k Gliedern der Reihe Teilsummen, versucht bei ihnen eine Regel zu entdecken und lässt anschließend k gegen Unendlich gehen. Bei der ersten Reihe sieht das so aus:
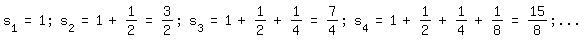
Die k-te Teilsumme ist gleich (2k -1 ) / 2k-1 und geht für k gegen Unendlich gegen 2.
Dasselbe ergibt sich, wenn der Term 1/(1-x) als unendliche Reihe geschrieben wird:*) Wählt man darin x=½, folgt
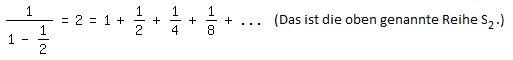
*) Wie beim schriftlichen Dividieren von Zahlen entsteht aus 1:(1-x) schrittweise 1+x+x²+x³+ ..., d. h. die geometrische Reihe.
Sehr oft ist es leider nicht möglich, anhand ihrer Teilsummen auf den Summenwert einer unendlichen Reihe zu schließen. Wer würde zum Beispiel damit erraten, dass gilt:
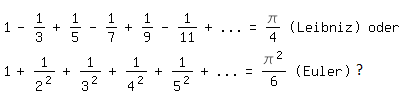
Für beide Reihen sind wesentlich stärkere mathematische Mittel erforderlich. Insbesondere die letzte Reihe als Lösung des so genannten "Basler Problems" machte den Schweizer zusätzlich berühmt, nachdem andere bekannte und einflussreiche Mathematiker verschiedener Länder daran gescheitert waren.
Übrigens: in diesem Jahr (2016) ist Leibniz' dreihundertster Todestag.
Kehren wir zur geometrischen Reihe Sg zurück und wählen x = -1, ergibt sich mit 1+x+x²+x³+ ... = 1/(1-x):
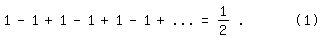
Die linke Seite hat keinen angebbaren Wert, denn ihre Teilsummen schwanken beständig zwischen 0 und 1, und auf der rechten Seite steht ein gewöhnlicher Bruch. Das Gleichheitszeichen ist ungültig und (1) somit falsch. Der Fehler entsteht dadurch, dass x, absolut gesehen, zu groß gewählt wurde. Damit die geometrische Reihe konvergiert, muss ∣x∣<1 sein.
Anmerkung: hier wird erwähnt, dass der italienische Mathematiker, Philosoph und Theologe Guido Grandi (1671-1742) das Ergebnis (1) für einen Beweis dafür hielt, dass "Gott die Welt aus dem Nichts" erschuf.
In unserer Zeit spielt (1) weiter eine gewisse Rolle, so zum Beispiel in einem Artikel von Spiegel Online Wissenschaft. Er enthält die Behauptung, dass auch noch gelte:
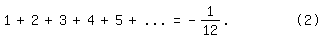
Links steht nach herkömmlichem Verständnis plus Unendlich, rechts etwas Endliches und sogar Negatives. Mit "+" kann nicht die gewöhnliche Addition gemeint sein, sondern vielleicht etwas anderes (s. u.); doch wird das in dem Artikel mit keinem Wort erwähnt.
Dieser gibt den Grundgedanken eines von zwei Physikern erstellten Videos wieder, in dem (2) "bewiesen" wird. Der Artikel lässt sich leichter und mehr in Ruhe lesen als das Video.
Begonnen wird mit der Behauptung, dass die mit A bezeichnete Reihe 1 - 1 + 1 - 1 + ... den Wert ½ habe, diesmal, unter Missbrauch des Wahrscheinlichkeitsbegriffs, als "Mittelwert" von 0 und 1. Dann wird eine Reihe B = 1 - 2 + 3 - 4 + 5 - 6 + ... definiert und nach unüblichem, "geschicktem Untereinandersetzen" behauptet, dass 2·B = A sei. Das ist offenbar falsch, denn 2·B ist gleich 2 - 4 + 6 - 8 + ... und nicht gleich 1 - 1 + 1 - 1 + ... .
Einleitend schreibt der Spiegel: "Den beiden Forschern macht es sichtlich Spaß, das absurde Ergebnis auf überzeugende Weise herzuleiten." Überzeugend ist das Ganze für mich keineswegs. (2) spiele in der physikalischen Stringtheorie eine Rolle, heißt es in dem Artikel weiter, und in dem Video wird die Seite eines Lehrbuches über dieses Gebiet kurz eingeblendet, auf der (2) als Gleichung zu sehen ist.
Die Zeile (2) stiftet unter Schülern und mathematisch interessierten Laien Verwirrung und wabert durch das Internet. Widersprochen wird ihr in dem englisch geschriebenen Blog "No, the sum of all the positive integers is not -1/12". Am Ende des Blogs (vor den sich anschließenden Kommentaren) wird auf die so genannte "Ramanujan-Summation" verlinkt. Ihren Namen hat sie nach dem vielfach als genial bezeichneten, früh verstorbenen indischen Mathematiker Srinivasa Ramanujan. Von ihm stammt (2), ursprünglich ohne besonderen Hinweis auf etwas Neues, Ungewohntes, vgl. hier, Abschnitt "Sum of divergent series".
Das Vorstehende wendet sich an den genannten Leserkreis, nicht an Fachleute, die sich vielleicht mehr für die Gültigkeit von (2) innerhalb einer bestimmten algebraischen Struktur, für die Ramanujan-Summation oder die analytische Fortsetzung der Zeta-Funktion interessieren, die in diesem Zusammenhang öfter genannt wird.
Worauf es mir hier ankommt, ist folgendes:
Man darf nicht mit etwas Unbestimmtem rechnen. Das geschieht im Internet zum Beispiel hier:
Sei S = 1 - 1 + 1 - 1 + ... , dann könne man (so heißt es dort) dafür auch schreiben:
1 - (1 - 1 + 1 - 1 + ...), d. h. S = 1 - S, woraus sich S=½ ergebe. Das aber ist die falsche Aussage (1).
Mit etwas Bestimmtem wie der für ∣x∣<1 konvergenten geometrischen Reihe
Sg = 1 + x + x2 + x3 + ... dagegen kann man sehr wohl rechnen. Oft wird das bei ihr so gemacht:
Sg - 1 = x (1 + x + x2 + x3 + ...), Sg - 1 = x Sg , woraus
1 + x + x2 + x3 + ... = 1/(1-x) folgt, wie es sein soll. Diese Herleitung ist einfacher als mit der Division 1:(1-x).
Dem o. g. Video folgt ein weiteres ("second proof and extra footage"). Deutlich sichtbar wird in ihm der Definitionsbereich der geometrischen Reihe 1/(1-x) = 1 + x² + x³ + ... falsch mit x<1 statt mit ∣x∣<1 angegeben.
Damit erhalten die Autoren, ebenfalls absurd, als Zwischenergebnis 1 - 2 + 3 - 4 + 5 - 6 + ... = 1/4 .
Auch durch das zweite Video werden nicht genügend aufmerksame, erfahrene, kritische Betrachter getäuscht, nur anders als durch das erste.
Ausführlich und mit zahlreichen Literaturangaben wird das Problem der Summe aller natürlichen Zahlen hier behandelt.
Auf dieser Seite werden
mehrere Summationsarten divergierender unendlicher Reihen vorgestellt, die von der gewöhnlichen Summation (Addition) abweichen. Eine Zeit lang war dort zu lesen: 1 - 1 + 1 - 1 +- ... "=" ½ , mit Anführungsstrichen um das Gleichheitszeichen.
Und hier wird der auf obskure Weise erhaltene Wert -1/12 dem Ausdruck 1+2+3+4+... nicht gleich gesetzt, sondern "zugeordnet", "mit ihm verbunden" [*]). (Zitat: "I have found a way to simply, and graphically explain how the series 1+2+3+4+ . . . is associated with (and not equal to) the number -1/12.") Siehe dazu auch noch hier.
Ergänzung: In diesem Video behauptet und "beweist" jemand, dass 1+2+3+4+...=-1/8 ist, im Gegensatz zu dem oben genannten Resultat der beiden Physiker. Dabei lässt er außeracht, dass im allgemeinen bei unendlichen Summen Klammern nicht beliebig gesetzt werden dürfen, vgl. z.B. hier.
Zurück zur Themenübersicht