Über das Sierpiński- und das Pascaldreieck
Das Sierpiński-Dreieck ist die bekannte Strichfigur:
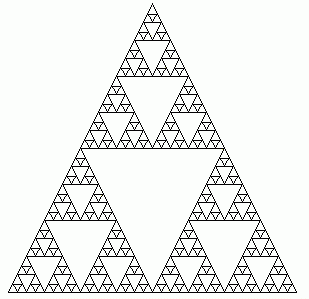
Man kann es auf (mindestens) zwei verschiedene Weisen annähern.
Zum einen mittels Zufallszahlen als Fraktal:

zum andern mit Hilfe des Pascalschen Dreiecks:

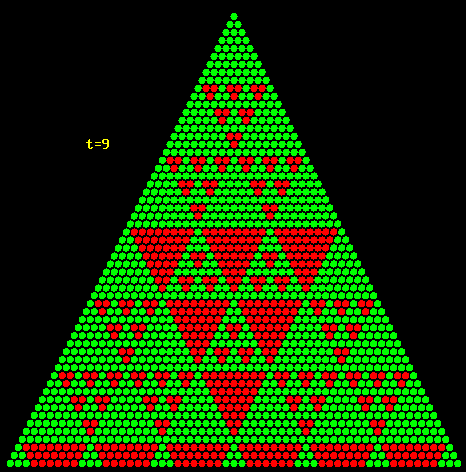
Bei dieser Figur werden die Binomialkoeffizienten nicht mit ihren Zahlenwerten wiedergegeben, sondern als kleine Kreise angedeutet. Die durch 5 teilbaren sind rot gefärbt.
Weitere Beispiele sind hier zu sehen:

Alle Teiler der rot markierten Binomialkoeffizienten sind Primzahlen >3.
Die Ähnlichkeit mit dem Sierpiński-Dreieck nimmt ab oder geht ganz verloren, wenn man zusammengesetzte Zahlen betrachtet,
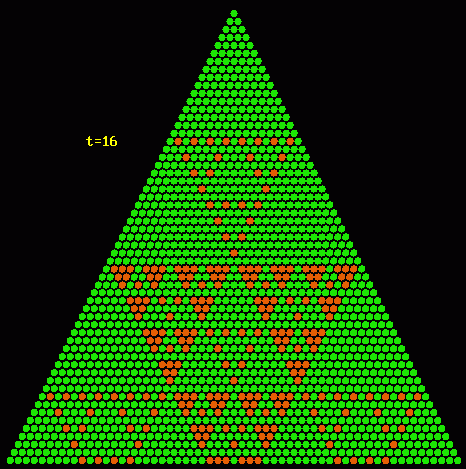
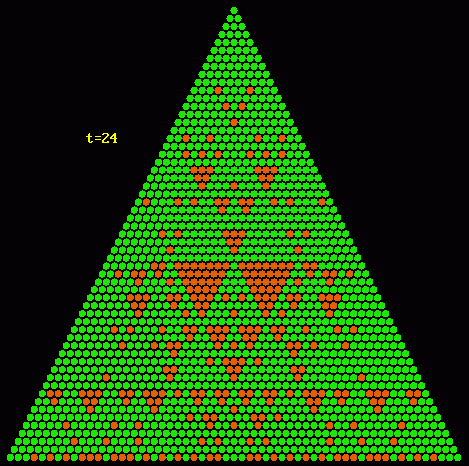
doch ist das nicht bei allen der Fall, wie die nächsten beiden Beispiele zeigen:
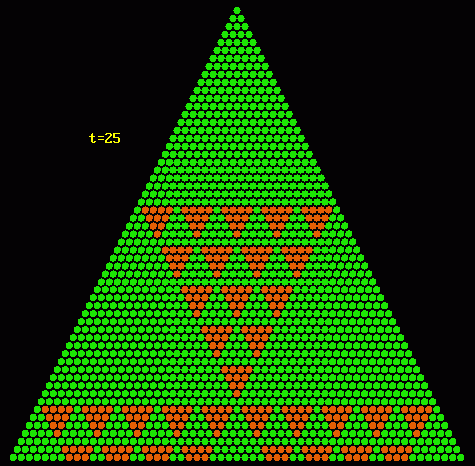
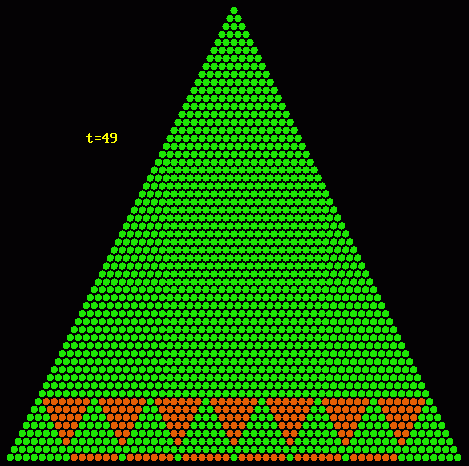
Durch sie kann man vermuten, daß sich sierpiński-ähnliche Pascaldreiecke ergeben, wenn die zusammengesetzten Teiler das Quadrat von Primzahlen sind. Leider widerlegt das folgende Beispiel diese Vermutung:
Auch scheint das Pascaldreieck für t=62, eine Zahl, die weder prim noch das Quadrat einer Primzahl ist, frei von Störungen zu sein und damit ebenfalls dem Sierpiński-Dreieck zu ähneln:

Selber kann ich das nicht klären.
Hans-Jürgen Hinweis: siehe auch den Nachtrag am Ende der folgenden Diskussionsbeiträge!
|
Re: Sierpiński- und
Pascal-Dreieck |
|
|
|
Re:
Sierpiński- und Pascal-Dreieck |
|
|
|
Re:
Sierpiński- und Pascal-Dreieck |
|
|
|
Re:
Sierpiński- und Pascal-Dreieck |
|
|
|
Re:
Sierpiński- und Pascal-Dreieck |
|
|
|
Re:
Sierpiński- und Pascal-Dreieck |
|
|
|
Re:
Sierpi?ski- und Pascal-Dreieck |
|
|
|
|
Re:
Sierpiński- und Pascal-Dreieck |
|
|
|
Re:
Sierpiński- und Pascal-Dreieck |
|
|
|
Re:
Sierpiński- und Pascal-Dreieck |
|
|
Nachtrag (nicht auf dem Matheplaneten): auf der von Rebecca verlinkten Wikipedia-Seite (Link 1) wird unter "Einzelnachweise 2" ein SPIEGEL-Artikel von 2009 zitiert (http://www.spiegel.de/fotostrecke/muschelgehaeuse~
fotostrecke-46503-8.html), aus dem das folgende Bild stammt:
Es zeigt, daß sierpiński-ähnliche Muster auch in der Natur vorkommen.
Zurück zur Themenübersicht, Teil 1