Was ist ein Punkt?
Punkte weisen ein paar Besonderheiten auf, an die man nicht immer denkt. Sie sind Gegenstand der folgenden Überlegungen.
Zeichnet man einen Punkt auf Papier oder an die Tafel, entsteht in Wirklichkeit eine kleine Fläche oder ein kleiner "Kreidehaufen". Punkte sind Gedankendinge und lassen sich weder sehen noch zeichnen. Manchmal werden sie "unendlich klein" genannt. Unsichtbar sind auch mit ihnen gebildete Strecken und Kurven, woran meist nicht gedacht wird.
Bei Euklid heißt es: "Ein Punkt ist, was keine Teile hat." Um besser zu verstehen, was hiermit gemeint ist, gehen wir von etwas Größerem, Handlichem aus, von einer Fläche oder einem Körper. Diese zerteilen wir fortlaufend, zuerst physisch, später nur noch in Gedanken. Bei Euklid findet dieser Teilungsprozeß ein Ende, denn wenn er sagt, daß der Punkt keine Teile hat, muß es nach dieser Auffassung etwas Kleinstes geben, das sich nicht mehr weiter zerteilen läßt. Ein "Geometrie-Atom", sozusagen, von gr. átomos=unteilbar, ähnlich wie in der Physik und Chemie, wo der aus der Antike stammende Begriff Atom inzwischen nicht mehr sachgerecht ist und nur noch aus Tradition beibehalten wird. Nach Euklid ist, so scheint es mir, ein Punkt etwas sehr Kleines, behält aber eine endliche Größe. Wo sie liegt, bleibt offen.
Der Gegensatz hierzu ist, daß der Teilungsprozeß immer weiter fortgesetzt wird, ohne jemals an eine Grenze zu stoßen. Dann bekommt der Punkt asymptotischen Charakter. Wer sagt, ein Punkt sei unendlich klein, redet nicht von einem feststehenden Objekt, sondern von einem, das nicht aufhört, immer kleiner zu werden. "Fertige" Punkte dürfte es dabei, streng genommen, gar nicht geben.
Auf diese beiden Möglichkeiten komme ich später zurück und wende mich jetzt etwas anderem zu.
Obwohl Punkte und Zahlen zunächst nichts miteinander zu tun haben, wird zwischen ihnen eine gedankliche Verbindung hergestellt, indem man auf einer Geraden oder Strecke bestimmte Punkte durch Zahlen markiert. Das geschieht zuerst mit den natürlichen Zahlen; dann kommen die Null und die negativen ganzen Zahlen hinzu. Auch Punkte innerhalb der Intervalle zwischen zwei ganzen Zahlen lassen sich so markieren: der dem Bruch 51/3=16/3 entsprechende Punkt zum Beispiel findet auf der Zahlengeraden ebenso seinen Platz wie jeder andere, der zu einer rationalen Zahl m/n gehört, wobei m und n ganze Zahlen sind (n ungleich null). Man spricht dabei auch kurz von "rationalen Punkten".
Stets kann man von zwei Brüchen das arithmetische Mittel bilden, welches selber wieder rational ist und somit einen weiteren rationalen Punkt ergibt, gleichgültig, wie eng die beiden, ihnen entsprechenden Ausgangspunkte benachbart sind. Oder anders ausgedrückt: in jedem noch so kleinen Intervall der Zahlengerade gibt es unendlich viele rationale Punkte. Man sagt deshalb auch, daß sie auf ihr dicht liegen.
Diese Ausdrucksweise suggeriert, daß die rationalen Punkte unmittelbar ohne Zwischenräume aufeinander folgen, doch ist sie, so verstanden, falsch. Betrachtet man (in Gedanken) nur die rationalen Punkte, bleiben Lücken auf der Zahlengerade, sogar unendlich viele. Sie werden von Punkten ausgefüllt, die irrationalen Zahlen entsprechen, d. h. solchen, die sich nicht als Brüche mit ganzzahligem Zähler und Nenner darstellen lassen. In einfachen Fällen, bei Quadratwurzeln, kann man ihren Ort auf der Zahlengerade nach dem Satz von Pythagoras mit Zirkel und Lineal konstruieren, wie das folgende Beispiel zeigt:
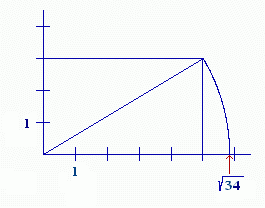
In der nächsten Figur
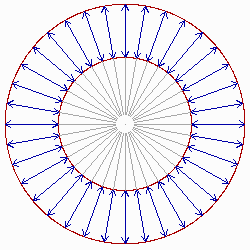
entspricht jedem, mit einem Doppelpfeil versehenen Punkt des inneren Kreises ein Punkt auf dem äußeren und umgekehrt. Da alle Kreispunkte (nicht nur die eingezeichneten) einen Pfeil aussenden und empfangen, ergibt sich zwangsläufig, daß beide Kreise aus gleich vielen Punkten bestehen, obwohl ihre Umfänge verschieden groß sind. Dies ist im ersten Moment sicherlich überraschend. Ohne die Zuordnungsfigur würde man eher denken, daß die äußere Kreislinie mehr Punkte enthält als die innere. Hierbei spielt offenbar die in der euklidischen Definition enthaltene Vorstellung eine Rolle, daß ein Punkt zwar etwas sehr Kleines, aber trotzdem Endliches ist.
Um dies noch ein wenig näher auszuführen, betrachten wir als Beispiel zwei konzentrische Kreise, deren Umfänge 10 und 12 cm lang sind. Die Größe eines "Punktes" wählen wir sehr gering: 1 "Mikromillimeter" = 1 nm. Dann besteht der kleinere Kreis aus 10 Milliarden und der größere aus 12 Mrd. solcher "Punkte". Am Anzahlverhältnis 1,2:1 ändert sich nichts, wenn wir die "Punktgröße" weiter verringern: auf 0,1 nm, 0,01 nm usw. Es ist auf diese Weise nicht möglich, daß daraus das Verhältnis 1:1 wird, wie es die obige Pfeilfigur nahelegt. Erst wenn die Punkte als unendlich klein angenommen werden (und dadurch ihre Anzahl bei beiden Kreisen ins Unendliche ansteigt), "verschwimmt" der Unterschied nach dem Motto: das 1,2-fache von Unendlich ist ebenfalls (nur) Unendlich.
Solche Überlegungen, bei denen alles auf den unbestimmten Begriff des Unendlichen abgedrängt wird, sind nicht sehr erfreulich und hinterlassen leicht ein ungutes Gefühl. Deshalb ist es auch nicht verwunderlich, daß die eingangs gestellte Frage Was ist ein Punkt? in Büchern und im Internet nicht oder nur spärlich behandelt wird. Wenn dies der Fall ist, wird, soweit ich sehe, kommentarlos Euklid zitiert, oder man rechnet den Punkt zu gewissen "Grundbegriffen", die sich nicht weiter erklären lassen.
Der Mathematiker Oskar Perron bemerkte dazu: „Ein Punkt ist genau das, was der intelligente, aber harmlose, unverbildete Leser sich darunter vorstellt.“ (Wikipedia)
Ergänzung (nicht auf dem Matheplaneten)
Nachtrag 2024: Zur Idee, Raum und Zeit könnten "körnig"sein: Neue Ansätze mit "Zellen" von Stephen Wolfram, dem Erfinder und Betreiber des vielbesuchten Mathematikforums"Wolfram Alpha". Er ist auch theoretischer Physiker und arbeitete an dem, was sich jetzt zu zeigen beginnt, seit fast fünfzig Jahren, siehe hier.
(Die von mir der leichteren Verständlichkeit verwendete Google-Übersetzung ist brauchbar. Hiermit meine ich nur einen Teil der Einleitung. Um das darauf Folgende zu verstehen, muss man nicht nur gut Englisch können, sondern vor allem sehr gut klassische wie moderne Mathematik und Physik, was bei mir leider nicht der Fall ist.)
Zurück zur Themenübersicht