Im folgenden habe ich einiges über die Parabel zusammengetragen, darunter Bekanntes und weniger Bekanntes, vielleicht zum Teil sogar Neues.
Sie ist eine ebene, nicht geschlossene Kurve, die zusammen mit der Ellipse und Hyperbel zu den Kegelschnitten gehört. Dieser Name erklärt sich dadurch, daß die drei genannten Kurven als Randlinien bei unterschiedlichen Schnitten eines geraden Kreiskegels mit einer Ebene auftreten.
In einem kartesischen Koordinatensystem mit den Achsen x und y lautet die einfachste Parabelgleichung y=x2; hierbei ist die Parabel nach oben geöffnet, und ihr Scheitelpunkt liegt im Ursprung. Streckt oder staucht man sie in y-Richtung, wird das durch die Gleichung y=ax2 beschrieben, und wenn der Scheitel nicht im Ursprung liegt, sondern die Koordinaten xS und yS hat, lautet sie y=a(x-xS)2+yS.
Die Parabel hat eine bemerkenswerte Eigenschaft, die beim Hohlspiegel und Autoscheinwerfer ausgenutzt wird: Lichtstrahlen, die parallel zu ihrer Symmetrieachse einfallen, werden in ein und denselben Punkt reflektiert, den Brennpunkt der Parabel:
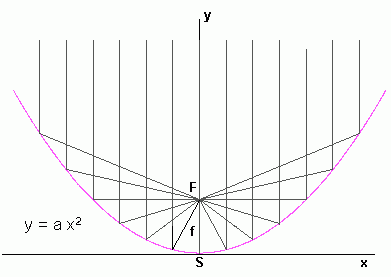
Wer wissen möchte, wie die Brennweite f mit dem Streckfaktor a zusammenhängt, kann von der klassischen, bereits aus der Antike stammenden Definition der Parabel ausgehen: "Eine Parabel ist die Menge aller Punkte P, deren Abstand zu einem festen Punkt F (dem Brennpunkt) und einer Geraden g (der Leitgeraden) gleich groß ist."
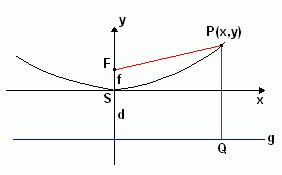
In dieser nur ungefähren Planfigur machen wir keine besonderen Voraussetzungen über den Abstand d der Leitgeraden von der x-Achse; Näheres ergibt die folgende Rechnung.
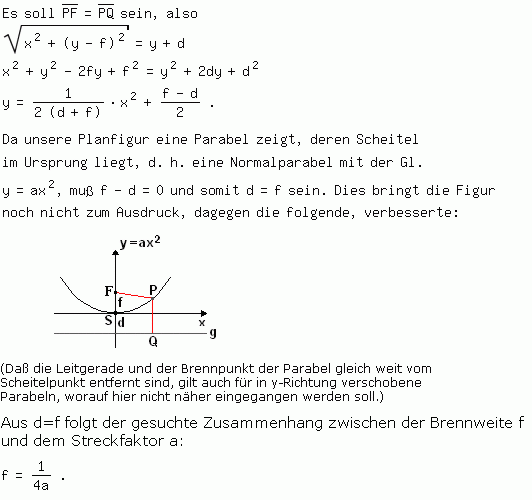
*
Während bei der klassisch definierten Parabel der Abstand eines Kurvenpunktes von einem festen Punkt stets gleich seinem Abstand von einer festen Geraden ist, wird in diesem Thread des Matheplaneten der Fall betrachtet, daß die beiden genannten Abstände im allgemeinen voneinander verschieden sind, aber ihre Summe konstant bleibt. Auch hierbei ergeben sich Parabeln, ebenso bei konstanter Differenz.
*
Dort wird auch noch diese Figur gezeigt:
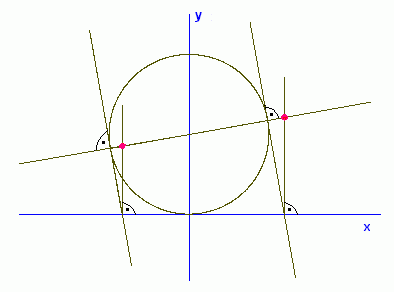
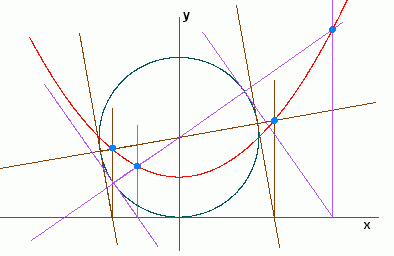
Sie enthält einen Kreis mit dem Radius R, dessen Mittelpunkt auf der y-Achse liegt und um R nach oben verschoben ist. Zieht man durch den Kreismittelpunkt eine beliebige Gerade g, ergeben sich zwei Schnittpunkte, in denen die Tangenten an den Kreis gezeichnet werden. Wo diese die x-Achse schneiden, wird jeweils das Lot errichtet. Die Schnittpunkte der Lote mit g liegen auf einer Parabel mit der Gleichung y=x2/(2R)+R/2. Sie ist in der nächsten Graphik mit einer zweiten Gerade durch den Kreismittelpunkt zu sehen. Dieser ist ihr Brennpunkt.
*
In der Physik begegnet uns die Parabel beim schrägen Wurf, falls der Luftwiderstand vernachlässigt werden kann. Das Bild zeigt zwei solcher Wurfparabeln:
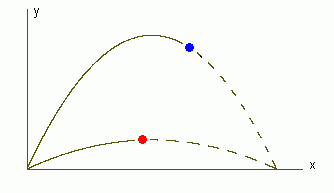
Sie deuten an, daß man bei betragsmäßig gleicher Abwurfgeschwindigkeit unter zwei verschiedenen Abwurfwinkeln zum selben Zielpunkt kommen kann ("Flachschuß", "Steilschuß"); beide Winkel ergänzen sich zu 90 Grad.
*
Dreht sich ein nicht ganz mit Wasser gefülltes, zylindrisches Gefäß mit konstanter Geschwindigkeit um seine Symmetrieachse, bewirkt das Zusammenspiel von Zentrifugal- und Schwerkraft, daß der Wasserspiegel zum Rand hin ansteigt und in der Mitte sinkt. Die Wasseroberfläche wird zu einem Paraboloid. Kennt man den Durchmesser des Gefäßes und die Anzahl der Umdrehungen pro Minute, läßt sich aus der gemessenen Steighöhe am Rand ein Näherungswert für die Erdbeschleunigung berechnen.
*
Zurück zur Mathematik. Bei den konformen Abbildungen unterwirft man gerne eine Schar von Geraden, die parallel zur imaginären Achse der z-Ebene verlaufen (z=x+iy), der Abbildung w=z2. Dadurch werden in der w-Ebene (w=u+iv) aus den Geraden nach links geöffnete Parabeln:
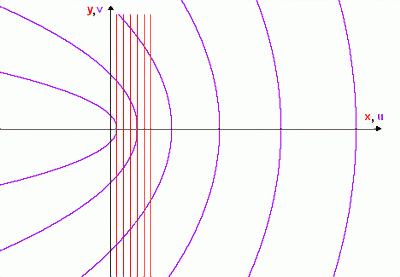
(Geraden: x=c, c=1,2,3,...,6; Parabeln: u=c2-v2/(4c2))
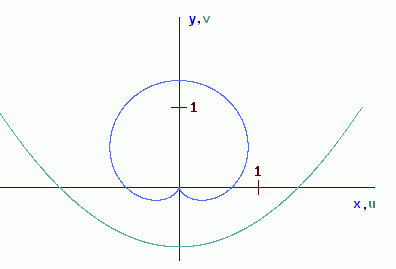
Als letztes betrachte ich die Kardioide mit der Gleichung
9(x2+y2)2-12(x2+y2)y-4 x2=0,
die in Polarkoordinaten x=r*cosφ , y=r*sinφ die einfachere Form
r=2(1+sinφ)/3 annimmt. Bildet man diese Kurve mit w=1/z
von der z- in die w-Ebene ab, entsteht die Parabel mit der
Gleichung v=u2/3-3/4:
Hans-Jürgen
(4.11.05)
|
Re: Über Parabeln |
|
|
|
Re:
Über Parabeln |
|
|
|
Re:
Über Parabeln |
|
|
|
Re:
Über Parabeln |
|
|
|
Re:
Über Parabeln |
|
|
|
Re:
Über Parabeln |
|
Hi, daß dieser Thread elementar verständlich ist, stimmt nicht ganz. Bei den zwei physikalischen Beispielen sind Kenntnisse in der Differential- und Integralrechnung erforderlich, und bei denen zur konformen Abbildung muß man etwas über komplexe Zahlen wissen. Sehr einfach hingegen, sogar ohne jegliche Rechnung, läßt sich die bei der ersten Figur mit dem Kreis indirekt gestellte Aufgabe lösen. Dort ist zu zeigen, daß die beiden roten Punkte auf einer Parabel liegen. Diese Figur wiederhole ich, der größeren Deutlichkeit halber zusätzlich eingefärbt: Nur mit dem Satz "Winkel, deren Schenkel aufeinander senkrecht stehen, sind gleich groß (oder ergänzen sich zu 180°)" und den Kongruenzsätzen zeigt man zuerst, daß das braune und das grüne Dreieck miteinander kongruent sind und anschließend dasselbe für das gelbe und das blaue Dreieck. Dadurch sind die Strecken TP und PQ gleich lang und somit auch die Strecken MP und PR. Der Punkt P ist also vom Kreismittelpunkt M und von der x-Achse gleich weit entfernt und deshalb Parabelpunkt, wie behauptet. Viele Grüße, Hans-Jürgen |