Rutscht der Fußpunkt einer an einer senkrechten Wand angelehnten Leiter ein Stück nach rechts, bewegt sich ihr oberes Ende um ein Stück nach unten, das im allgemeinen nicht gleich groß ist:
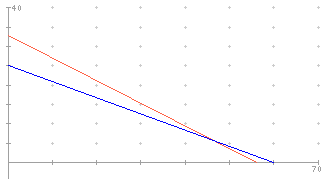
(Die beiden, von der Leiter und den Achsen gebildeten, rechtwinkligen Dreiecke haben dieselbe Hypotenuse. Es ist 33²+56²=65² und 25²+60²=65².)
Zeichnet man mehrere verschiedene Leiterpositionen ein und nimmt zur Vervollständigung den 2. bis 4. Quadranten mit hinzu, entsteht folgende Figur:
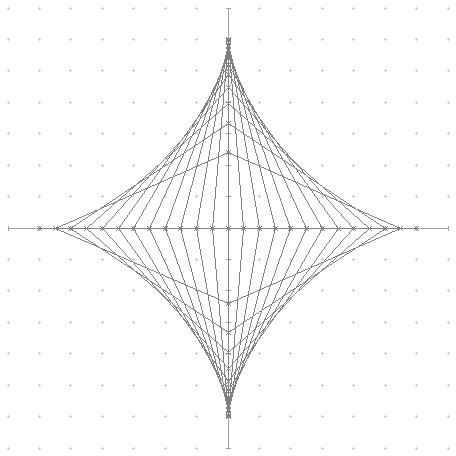
Eingehüllt wird sie von einer Astroide (Sternkurve).
Deren Gleichung aufzustellen, erscheint mir vom Gedanklichen her nicht ganz einfach. Im Studium und in Analysisbüchern wird die Hüllkurve einer Kurvenschar (auch Einhüllende oder Enveloppe genannt) oft nur oberflächlich oder gar nicht behandelt, manchmal auch zu weitschweifig, so daß man leicht den Überblick verliert. Auch die folgende Erklärung hat sicherlich ihre Schwächen.
Bei einer Schar gleichartiger Kurven oder Geraden, die sich durch einen gewissen Parameter p voneinander unterscheiden, enthält ihre Funktions- bzw. Relationsgleichung nicht nur die Variablen x und y, sondern auch p, so daß man sie in der Form F(x,y,p)=0 schreiben kann. Zwei Nachbarkurven der Schar mit den Parameterwerten p und p+h werden von der gesuchten Hüllkurve an verschiedenen Punkten berührt. Setzt man die partielle Ableitung von F nach p:
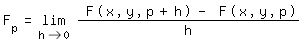
gleich 0, bedeutet dies anschaulich, daß sich die beiden Berührpunkte unbegrenzt einander annähern und gemeinsam einen Punkt der Hüllkurve ergeben - falls diese existiert. Das ist nicht immer so, etwa bei konzentrischen Kreisen oder hier:
Für das Aufstellen der Enveloppengleichung ist die Bedingung Fp = 0 zwar notwendig, aber nicht hinreichend. Ihre formale Anwendung führt bei diesem Beispiel zum Ergebnis y=0, d. h. die "Hüllkurve" ist die x-Achse!
Solche Bedenken bestehen bei der variabel angelehnten Leiter nicht. Diese hat ja eine richtige Enveloppe, und wir fragen nach ihrer Gleichung. In der folgenden Figur
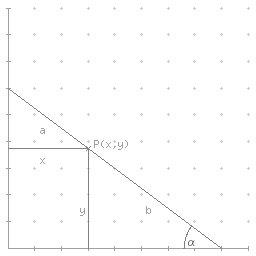
wird die Leiterlänge c durch einen Punkt P(x,y) in zwei Abschnitte a und b geteilt. Dabei gilt:
woraus sich
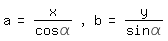
ergibt, was mit c=a+b auf
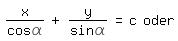
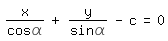
führt. Die letzte Zeile hat die oben erwähnte Form F(x,y,p)=0; der Winkel α ist hier der Parameter, so daß wir auch
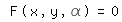
schreiben können.
Die partielle Ableitung von F nach α und Nullsetzen derselben liefert
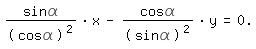
Die daraus sich ergebende Gleichung
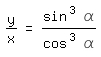
wird durch das Gleichungspaar
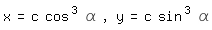
erfüllt und beschreibt die Astroide in Parameterform. Diese erhält man auch, wenn die Astroide als Rollkurve (Hypozykloide) erzeugt wird. Dabei bedeutet α den Wälzwinkel des Rollkreises.
Die parameterfreie Darstellung der Sternkurve folgt durch Ziehen der Kubikwurzel aus x und y mit anschließendem Quadrieren und unter Berücksichtigung von sin²α + cos²α = 1:
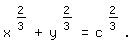
Nun soll als nächstes die Leiter nicht mehr hin- und herrutschen, sondern unter einem festen Winkel ß der Wand lehnen:
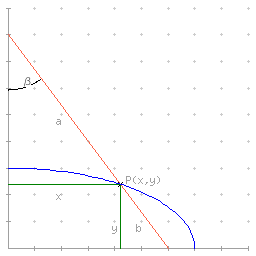
Dann gilt für einen Leiterpunkt P(x,y), der wiederum die Leiter in die Abschnitte a,b aufteilt:
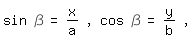
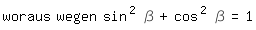
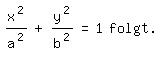
Das bedeutet: P liegt auf einer Ellipse mit den Halbachsen a und b. (In der obigen Figur teilt P(4,;2,4) die Leiter im Verhältnis 7:3.)
Wählt man weitere Leiterpunkte mit unterschiedlichen Teilungsverhältnissen a:b, ergibt sich eine Ellipsenschar:
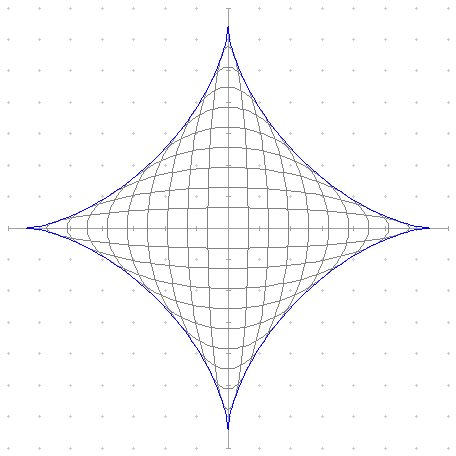
Einhüllende ist auch hier die Sternkurve. Dies läßt sich ebenfalls, am besten mit Polarkoordinaten, leicht beweisen. An die Stelle von Fp = 0 tritt dann eine andere, etwas kompliziertere Bedingung.
Zurück zur Themenübersicht