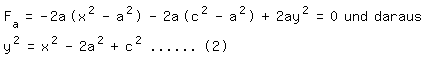Über Hüllkurven (Einhüllende, Enveloppen)
Kürzlich wurde hier [1] gefragt, wie man zu einer gegebenen Kurvenschar die
Einhüllende, auch Hüllkurve oder Enveloppe genannt, ermittelt. Der Fragesteller
(oder die Fragestellerin?) meinte, daß die Erklärungen dazu im Internet nicht
ausreichen. Das mag sein, und da das recht reizvolle Thema in der Schule wie
auf der Uni nur verhältnismäßig selten behandelt wird, greife ich es hier, zum
Teil mich selber zitierend, erneut auf.
In [2] schrieb ich:
Bei einer Schar gleichartiger Kurven oder Geraden, die sich durch einen
gewissen Parameter p voneinander unterscheiden, enthält ihre Funktions- bzw.
Relationsgleichung nicht nur die Variablen x und y, sondern auch p, so daß man
sie in der Form F(x,y,p)=0 schreiben kann. Zwei Nachbarkurven der Schar mit den
Parameterwerten p und p+h werden von der gesuchten Hüllkurve an verschiedenen
Punkten berührt. Setzt man die partielle Ableitung von F nach p:
![]()
gleich 0, bedeutet dies anschaulich, daß sich
die beiden Berührpunkte unbegrenzt einander annähern und gemeinsam einen Punkt
der Hüllkurve ergeben - wenn diese existiert. Dies ist nicht immer der
Fall, etwa bei konzentrischen Kreisen, bei einer Schar von Cassinischen Kurven
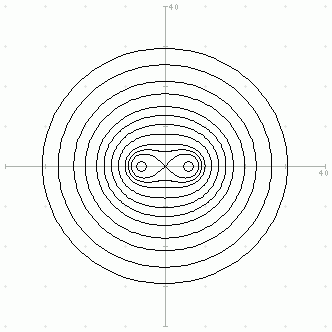
oder hier:
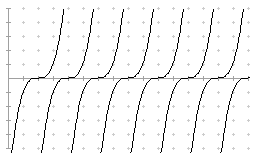
Für das Aufstellen der Enveloppengleichung ist die Bedingung Fp=0
zwar notwendig, aber nicht hinreichend. Ihre formale Anwendung führt bei dem
letzten Beispiel zum Ergebnis y=0, d. h. die "Hüllkurve" ist die
x-Achse!
Anders ist es bei der folgenden Kreisschar
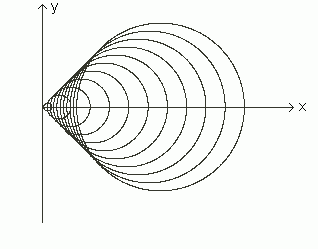
Sie hat eine Einhüllende, und am Ende von [1] wird rechnerisch gezeigt,
daß diese von den Winkelhalbierenden des 1. und 4. Quadranten gebildet wird.
Hier, in diesem Beitrag, sollen, anstelle in x-Richtung verschobener Kreise,
zum Ursprung konzentrische Ellipsen mit der Gleichung
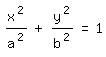
betrachtet werden, und zwar in zwei verschiedenen Ausführungen.
Bei der ersten Kurvenschar nehmen die großen Halbachsen um dieselbe Strecke zu,
um die sich die kleinen verringern, so daß ihre Summe gleich groß bleibt:
a+b=c=const. Dann gilt für diese Ellipsen
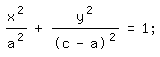
a ist der Parameter der Schar; c wird fest vorgegeben.
Anders geschrieben, lautet die Gleichung
![]()
F, partiell nach a abgeleitet, ergibt
![]()
Dies führt in Verbindung mit (1) auf x2=a3/c, und durch
Einsetzen in (1) ergibt sich y2=(c-a)3/c.
Zieht man in diesen zwei Gleichungen beiderseits die Kubikwurzel,
entsteht x2/3=a/c1/3 und y2/3=(c-a)/c1/3,
woraus
![]()
folgt. Dies ist die Gleichung der Sternkurve oder Astroide:
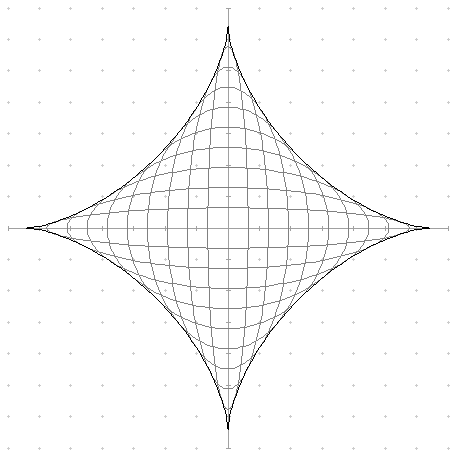
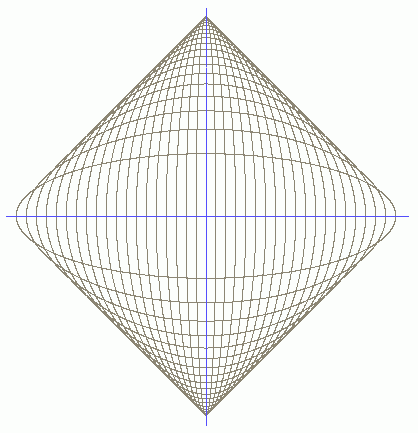
Bei der zweiten angekündigten Ellipsenschar soll nicht mehr gelten
b=c-a, sondern b2=c2-a2. Dann folgt:
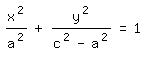
Daraus entnehmen wir a2=cx und setzen es, weil die Gleichung der
Einhüllenden nicht mehr den Parameter a enthalten darf, in (2) ein:
![]()
Hieraus folgt y=x-c und y=-x+c; das sind Gleichungen von Geraden, die die
Achsen unter 45° schneiden. Zwei weitere, zu ihnen symmetrisch verlaufende
ergeben sich, weil aus a4=c2x2 auch a2=-cx
folgt. Insgesamt ist die Hüllkurve bei dieser Ellipsenschar ein Quadrat:
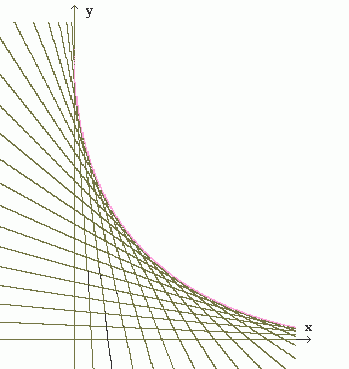
Untersucht habe ich auch die Kurvenschar mit der Gleichung
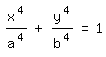
und b4=c4-a4. Die Kurven ähneln abgerundeten
Rechtecken, und die Hüllkurve ist ein Kreis:
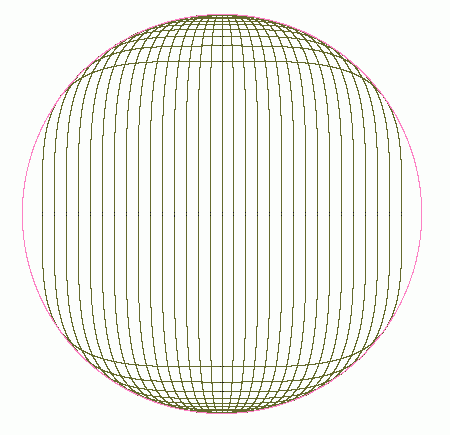
Zum Abschluß gehe ich mit dem Exponenten 4 des letzten Beispiels ein paar
Schritte zurück und betrachte die Geradenschar mit
![]()
Wiederum ist es unser Ziel, aus diesen beiden Gleichungen eine weitere
Gleichung zwischen x,y und c zu gewinnen, die den Parameter a nicht mehr
enthält. Sie beschreibt die Hüllkurve.
Dabei ergibt sich y=(c-a)2/c und x=a2/c. Potenziert man
beiderseits mit ½ und faßt zusammen, entsteht
![]()
Die rote Linie in der Figur folgt der Gl.
![]()
Hans-Jürgen
[1] Berechnung der Hüllkurve einer Funktionsschar
[2] Die Leiter und die Sternkurve
|
Re: Über Hüllkurven (Einhüllende, Enveloppen) |
|
|
Zurück zur Themenübersicht, Teil 1