|
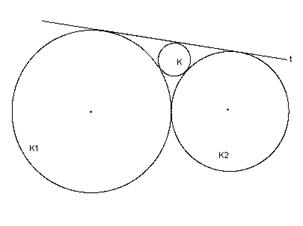
Re: Berührkreisproblem |
|
|
|
Re:
Berührkreisproblem |
|
|
|
Re:
Berührkreisproblem |
|
|
|
Re:
Berührkreisproblem |
|
|
|
Re:
Berührkreisproblem |
|
|
|
Re:
Berührkreisproblem |
|
|
|
Re:
Berührkreisproblem |
|
|
Zurück zur Themenübersicht