"Ein 16-Liter-Gefäß A ist ganz mit Wein gefüllt. Sein Inhalt soll ohne Verwendung einer Waage, eines Maßstabs mit Skala u. dgl. halbiert werden. Zur Verfügung stehen nur zwei leere Gefäße B und C, die 10 bzw. 6 Liter fassen."
Aufgaben dieser Art findet man öfter als Rätsel in Büchern über unterhaltsame Mathematik. Zu lösen sind sie dadurch, dass die Flüssigkeit aus dem großen Gefäß zum Teil in die kleineren gegossen wird und man sie anschließend in verschiedenen Portionen mehrfach hin- und hergießt.
Im vorliegenden Fall sieht eine mögliche Lösung so aus:
A B C
16 0 0 (Ausgangssituation)
6 10 0
6 4 6
12 4 0
12 0 4
2 10 4
2 8 6
8 8 0 (Halbierung erreicht)
In seinem Buch "Kaleidoskop der Mathematik" gibt Hugo Steinhaus ein interessantes mechanisches Verfahren an, bei dem eine angestoßene Kugel auf einem besonders geformten Billardtisch automatisch die Lösung findet.
Die von ihm verwendeten Gefäße fassen 12, 7 und 5 Liter; das größte ist ganz mit Wein gefüllt, die beiden anderen sind leer. Der Billardtisch ist ein Parallelogramm mit den Winkeln 60° und 120°. Mit Bezug auf diese Figur:
schreibt Steinhaus:
"Die Aufteilung des Weins in zwei gleiche Teile verläuft folgendermaßen: In die linke untere Ecke des Billardtisches legt man eine Billardkugel und gibt ihr einen Stoß in Richtung der unteren Kante; so lange nun die Billardkugel geradeaus rollt, fließt, wie die Abb. zeigt, der Wein aus dem großen Gefäß in das mittlere. Trifft die Billardkugel auf die Kante und ändert sie in Übereinstimmung mit den Gesetzen der Mechanik ihre Richtung, so bleibt der Stand des Weines im großen Gefäß ungeändert; dagegen wächst er im kleinen auf Kosten des mittleren usw. Dies geht so lange vor sich, bis der Wein in gleiche Teile aufgeteilt ist. Die Abb. zeigt die gebrochene, aus 11 Stücken bestehende Bahn der Billardkugel; der Endpfeil markiert die Stelle, wo die Halbierung des Weins erreicht wird. Somit sind 11 Umfüllungen notwendig, und das ist die einfachste Lösung."
Weiteres wird nicht erklärt, insbesondere nicht, worauf die Idee mit dem speziellen Billardtisch beruht. Dies soll im folgenden geschehen.
Als Ausgangspunkt wähle ich den Satz von Viviani:
Fällt man von einem Punkt P im Innern oder auf dem Rand eines gleichseitigen Dreiecks das Lot auf die Seiten, so ergeben die Längen aller drei Lote zusammen die Länge der Dreieckshöhe: a+b+c=h.
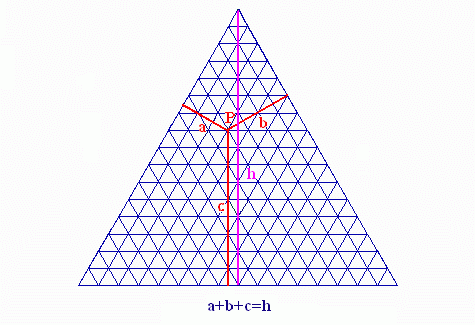
Auf den Beweis dieses Satzes werde hier verzichtet; er ist eine nette kleine Übung.
Die letzte Figur wenden wir auf unser Eingangsbeispiel an, und zwar ohne die Kugel. Die Länge der Lote a,b,c sollen den wechselnden Inhalten der Gefäße A,B,C nach der obigen Liste entsprechen. Der Anfang 16;0;0 bedeutet, dass a 16 Einheiten lang ist, während b=c=0 gilt. Wir beginnen deshalb unten rechts beim Punkt 0:
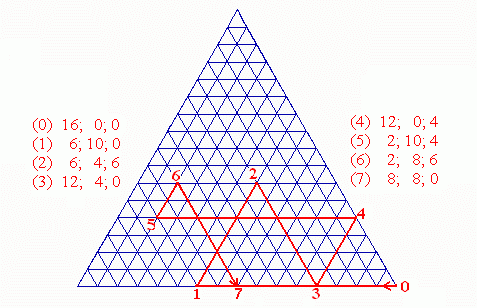
Von hier aus gehen wir zum Punkt 1 mit a=6, b=10 und c=0, dann nach Punkt 2 mit a=6, b=4, c=6 und so weiter bis Punkt 7, der die letzte Zeile der Tabelle wiedergibt.
Einen großen Teil des Dreiecks hätten wir zur Lösung der Aufgabe gar nicht gebraucht. Lässt man alles Überflüssige weg, ergibt sich eine Figur ähnlich der von Steinhaus, die damit begründet wird.
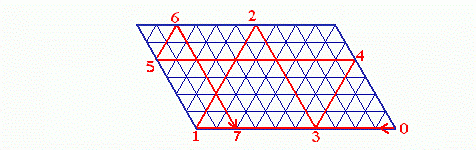
Anmerkung: Dass sich die Billardkugel nach der Ankunft beim 120°-Winkel so bewegt, wie es die Strecke von (1) nach (2) anzeigt und von Steinhaus behauptet wird, kann ich mir nicht recht vorstellen. Ich habe eher das Gefühl, dass sie in diesem Fall am Rand des Billardtisches weiterrollt, anstatt scharf abzubiegen. (Ansonsten, d. h. wenn sie die Bande mittendrin an anderen Stellen trifft, folgt die Kugel, wie vorausgesetzt, dem Reflexionsgesetz "Einfallswinkel=Ausfallswinkel".) Selbst wenn der Steinhaussche "Analogrechner", wie man ihn nennen könnte, in der Praxis funktioniert, ist das graphische Verfahren durchaus von Nutzen. Niemand wird sich zur Lösung von Umfüllaufgaben extra einen Billardtisch mit 60- und 120-Grad-Winkeln bauen; ein gleichseitiges Dreieck mit Gitternetzlinien ist dagegen schnell gezeichnet, wenn man durch Nachdenken und Probieren nicht weiterkommt.
Da man zu Anfang einen Teil des Inhalts des größten Gefäßes entweder in das mittlere oder das kleinste Gefäß gießen kann, gibt es bei den Umfüllaufgaben dieser Art stets zwei Lösungen. In unserem Beispiel sieht die zweite so aus:
16 0 0
10 0 6
10 6 0
4 6 6
4 10 2
14 0 2
14 2 0
8 2 6
8 8 0
Bei ihr bewegt sich die Kugel auf dem gedachten Billardtisch anfangs nicht an der unteren Kante von rechts nach links, sondern an der rechten schräg nach oben:
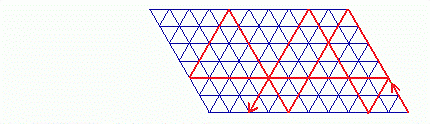
Hierbei benötigt man eine Umfüllung mehr als bei der ersten Lösung (8 statt 7).
ein weiteres Beispiel
Zurück zur Themenübersicht