|
Über Reihen für Potenzen von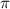 
Im Zusammenhang mit Fourier-Reihen (und sicherlich auch auf andere Weise)
erhält man Reihen wie diese:
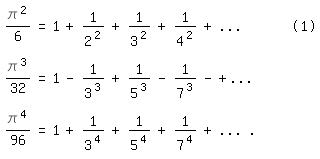
Die Reihe (1) erregte seinerzeit großes Aufsehen. Sie ist die Lösung
des "Basler Problems", welches aus der Frage bestand: "Wie
groß
ist die Summe der Kehrwerte der Quadrate aller natürlicher Zahlen?"
Gestellt wurde die Aufgabe bereits 1644 in Italien, und mehrere
namhafte Forscher bemühten sich vergeblich um ihre Lösung, darunter
Angehörige der Schweizer Mathematikerfamilie Bernoulli.
Erst im Jahre 1733 fand Leonhard Euler, ebenfalls Schweizer,
das obige Ergebnis (1), und zwar ohne Verwendung von Fourier-Reihen.
Wie er dabei vorging, wird u. a. bei Wikipedia erklärt.[1]
Diese Erklärung ist kurz und nicht für jeden unmittelbar verständlich.
Bei ihr wird von einer Produktdarstellung Gebrauch gemacht,
die auch von Euler stammt.
In der Folge bewies Euler die Gültigkeit der Reihe (1) mehrfach
auf verschiedene Weise. Sein ursprünglicher Ansatz wird im
Internet
in [2] zitiert. Entscheidend ist dabei der dort ohne Begründung
angeführte Satz:
"Bei einer algebraischen Gleichung, deren absolutes Glied den Wert 1
hat, ist der Koeffizient des Gliedes mit der ersten Potenz der
Unbekannten gleich der negativen Summe der reziproken Werte der
Gleichungswurzeln."
(Weiteres dazu s. unten.)
Selber möchte ich das Verfahren an einem anderen Beispiel demonstrieren.
Nach demselben Schema kann man auch Reihen für 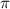selbst
herleiten,
d. h. für die erste Potenz, zum Beispiel aus der Gleichung sin x = 1/2:
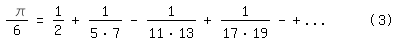
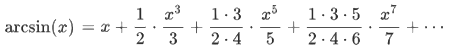
Sie sieht einfacher aus als die Arkussinusreihe für x=1/2 mit demselben Grenzwert
p/6,
ist leicht zu programmieren und konvergiert schneller als die Leibnizreihe (Vergleich,
jeweils 10000 Summanden: Leibniz: 3,14149...; (3): 3,141592652...; 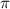=3,141592653...),
ist aber ebenfalls ungeeignet, wenn man viele Nachkommastellen von 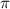haben
möchte.
Abschließend ein möglicher Anfang einer Begründung für den weitgehend
unbekannten Satz von Euler:
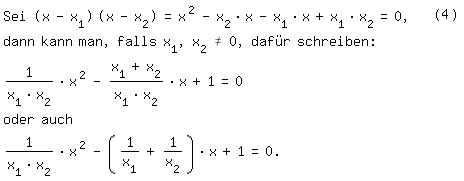
In Worten: Der Koeffizient von x ist gleich der negativen Summe
der Kehrwerte der Lösungen der Gleichung (4).
Entsprechendes gilt, falls
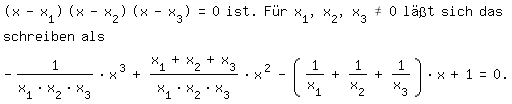
Auch hier haben wir dasselbe, und ich sehe keinen Grund dafür, daß es bei Gleichungen
4., 5., ... Grades
anders sein wird. Eulers Ausdehnung auf Gleichungen vom Grad "unendlich"
wurde von Kritikern als "kühn" und "gewagt" bezeichnet.
[1] de.wikipedia.org/wiki/Basler_Problem
[2] http://archiv.ub.uni-heidelberg.de/volltextserver/13424/1/staeckel_Euler_Abh.pdf S. 42
Weitere Literatur:
[3] Peter Mäder: Mathematik hat Geschichte, Metzler Schulbuchverlag, ISBN 3-507-03363-1, 1992, S. 49: "Aus der Gleichungstheorie wußte Euler, dass die Summe der reziproken Wurzeln der Gleichung
1+a1x+a2x²+....+anxn=0 gleich -a1
ist." Inhaltlich findet sich dies mit anderen Worten bei Euler selbst in:
[4] "Über die Summen reziproker Reihen", S.5, §6. (Übersetzung aus dem Lateinischen)
*
Ergänzung, nicht auf dem Matheplaneten:
In der dortigen Diskussion über diesen Artikel wurde meine Bemerkung zu Gleichungen 4.,5.,.... Grades von einem Mitglied als "sehr schlechter Stil" kritisiert und Eulers Vorgehensweise kurzerhand als "falsch" bezeichnet. (Das glaube ich nicht und denke vielmehr, dass Eulers Beweisführung im wesentlichen, abgesehen von gewissen Schwächen, die erst später bemerkt wurden, korrekt ist. Sonst wäre er nicht zum richtigen Ergebnis gekommen, das vorher niemand kannte oder vermutete.)
Im Gegensatz zu der obigen MP-Kritik beurteilte der berühmte amerikanische Mathematiker ungarischer Herkunft George Pólya in diesem Buch (Leseprobe, Seiten 43 ff und 60 ff) Eulers ersten Beweis (um den es hier geht) einfühlsam und verständnisvoll. –
Da bei mir, anders als bei Euler, nicht sinus x durch x geteilt wird, gibt es keine Schwierigkeiten für x=0. Zwar erhält man nicht die Reihe für p²/6, sondern für p²/8, doch lässt sich erstere leicht aus letzterer gewinnen:
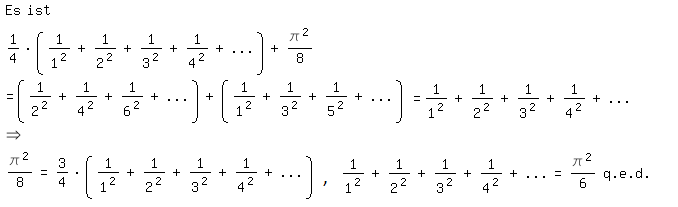
Ein weiteres Beispiel auf demselben Wege wie oben, diesmal ausgehend von cos x = 1/2,
ist die Reihe:
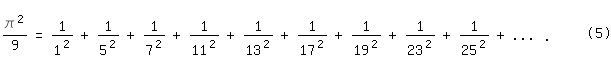
Sie und die Reihe (3) werden im Internet anscheinend nicht erwähnt.
|