Die in der Überschrift genannte Kurve gehört zu meinen Lieblingskurven. Nicht, daß sie unter all' den Kurven, die seit der Antike und besonders ab dem 17. Jahrhundert entdeckt wurden [1], die schönste ist. Vielmehr zeichnet sich die Kardioide dadurch aus, daß sie auf mindestens ein halbes Dutzend verschiedene Arten zustande kommt. Darüber soll im folgenden berichtet werden.
Nicht immer muß die Kardioide künstlich erzeugt werden. Bisweilen entsteht sie oder eine ihr ähnliche Kurve von allein, wenn Licht an runden Gegenständen reflektiert wird. Dies wird auf dem Matheplaneten ausführlich in [2] behandelt.
Die wohl bekannteste Definition der Kardioide ist diese: auf einem festen Kreis rollt außen ein ebenso großer Kreis mit einem Zeichenstift ab. Was sich hierbei ergibt, kann man auf der Wikipedia-Seite [3] durch Anklicken der Figur oben rechts ansehen. Die folgende Figur zeigt eine "Momentaufnahme" der animierten Graphik:
Die auf der Wikipediaseite anschließend angegebene Kardioidengleichung in kartesischen Koordinaten:
(x²+y²)² - 2ax(x²+y²) - a²y² = 0 (1)
paßt nicht dazu - die rote Kurve geht nicht durch den Ursprung.
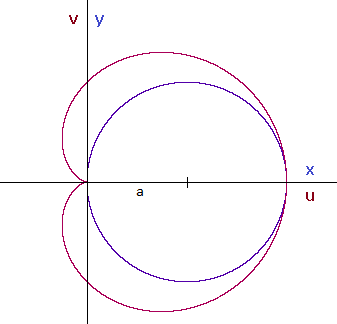
Die Figur, die (1) erfüllt, sieht so aus:
Anmerkung: Die in Lehrbüchern und im Internet, z. B. hier [4], zu findende Herleitung von Gl. (1) anhand einer detailreichen Planfigur ist recht mühevoll. Nur durch Rechnung, ohne Rückgriff auf die geometrische Anschauung, ergibt sich (1) aus einem anderen Ansatz am Ende dieses Artikels.
Werden Polarkoordinaten r, φ mit r=√(x²+y²) und tan φ = y/x eingeführt, entsteht aus (1)
r = a ( 1 + cos φ). (2)
Damit ergibt sich eine Möglichkeit, die Kardioide punktweise mit Zirkel und Lineal zu konstruieren:
Hierzu zeichnet man einen beliebigen Radius a=OK, fällt von K das Lot mit dem Fußpunkt F auf die y-Achse und verlängert die Strecke OK um die Strecke FK. Dann hat der Punkt P vom Ursprung O den Abstand r = a (1 + cos φ) wie in (2). Links von der y-Achse ist bei K die Strecke FK nicht nach außen, sondern nach innen abzutragen, weil hier a cos φ negativ wird:
Auf der genannten Wikipediaseite wird eine einfachere Konstruktionsmöglichkeit für die Kardioide angegeben:
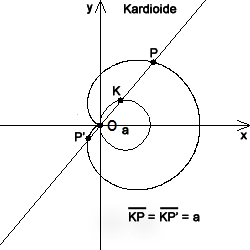
Hiernach soll man vom Ursprung O aus eine Kreissehne zum beliebig gewählten Punkt K ziehen und diese um a verlängern. Daß der dabei erreichte Punkt P, wie behauptet, auf einer Kardioide liegt, läßt sich so begründen:
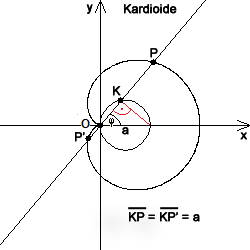
Die rote Strecke bildet mit der Strecke OK bei K einen rechten Winkel (Thales); somit gilt OK = a cosφ, und wir erhalten mit r=OP:
r = a (1+cosφ).
Dies ist wieder die Kardioidengleichung (2), wobei aber jetzt a nicht den Radius, sondern den Durchmesser des Kreises bedeutet.
Bei der Lichtreflexion an der Innenfläche zum Beispiel einer Teetasse entsteht die Kardioide als Hüllkurve von Lichtstrahlen, wenn das Licht, was nur selten vorkommt, von einem Punkt am Tassenrand ausgeht. Fallen dagegen die Lichtstrahlen einer weit entfernten Quelle (näherungsweise) parallel ein, ergibt sich ein Teil einer Nephroide. Dieser sieht ähnlich wie eine Kardioide aus:
(Kopie einer fedgeo-Graphik von Matroid im Diskussionsteil von [2].)
Anmerkung: die Nephroide entsteht ebenfalls durch Abrollen eines Kreises auf einem Kreis. Der Durchmesser des Rollkreises ist dabei halb so groß wie der des festen Kreises. [5]
Eine Kardioide läßt sich auch als Hüllkurve einer Kreisschar gewinnen [6]:

Und sie umschließt den Hauptteil des fraktalen "Apfelmännchens":
Wie das mathematisch begründet wird, wüßte ich gern.
Eine weitere Möglichkeit, die Kardioide zu erzeugen, ist die Verwendung der komplexen Abbildung w=c2/z mit z=x+iy, w=u+iv, c=const. Hierbei ergibt sich:
Nimmt man nur das untere Vorzeichen, ist
r = c2⋅2a(1+sinφ),
und das entspricht der Kardioidengleichung (2) mit dem Unterschied, daß wir jetzt sinφ anstelle von cosφ haben. c2 ist ein Maßstabsfaktor, mit dem sich die als Bildkurve der Parabel entstandene Kardioide vergrößern oder verkleinern läßt.
Das nächste Bild zeigt als Beispiel den Fall a=1/2, b=-1/(4a)=-1/2, c=3/2:
Auch die gebrochen quadratische Abbildung w=c3/z2 liefert Kardioiden:
Das ist in der u,v-Ebene die Kardioidengleichung (1).
Ein Beispiel zeigt abschließend dieses Bild:
Hans-Jürgen
[1] Eine kleine Auswahl findet man hier.
[2] Geometrie in der Teetasse
[3] http://de.wikipedia.org/wiki/Kardioide
[4] http://www.math.uni-magdeburg.de/~hoeding/Analysis0708/folie10_5_16a.jpg
[5] http://upload.wikimedia.org/wikipedia/commons/c/c5/Nephroid.gif
[6] Die Kardioide als Hüllkurve
|
Re: Nochmals: die Kardioide |
|
|
|
Re:
Nochmals: die Kardioide |
|
|