Über Logarithmen
Logarithmen waren über Generationen Unterrichtsstoff in der Realschule und im Gymnasium. Seit dem Aufkommen der Taschenrechner gerieten sie zunehmend in den Hintergrund und werden höchstens noch kurz am Rande erwähnt, etwa bei der Frage, was eigentlich auf dem Rechner die Tasten LOG und LN bedeuten. Dabei handelte es sich bei ihnen Jahrhunderte lang um ein überaus nützliches Werkzeug zur Lösung numerischer Aufgaben in Naturwissenschaft und Technik, an dessen Weiterentwicklung und Verbreitung in Form von Tabellen (Logarithmentafeln) Mathematiker und Buchverlage mit großem Eifer beteiligt waren.
Auf der Wikipediaseite [1] über Logarithmen steht dieses Zitat von Laplace:
"Durch die Arbeitserleichterung infolge der Verwendung von Logarithmen wird das Leben der Astronomen verdoppelt."
Es unterstreicht die Bedeutung, die diese Zahlenart seinerzeit hatte.
Die Wikipediaseite ist mit ihren Informationen über die Herkunft und die Eigenschaften der Logarithmen sehr reichhaltig, so daß ich mich auf ein paar Einzelheiten beschränken möchte, die dort nicht erwähnt werden.
Das Wort Logarithmus ist aus den beiden griechischen Wörtern "logos" und "arithmos" zusammengesetzt, wobei das letztere "Zahl" bedeutet. Logos läßt sich mit "Wort" übersetzen, doch gibt es mindestens weitere zehn, zum Teil recht unterschiedliche Möglichkeiten dafür. Eine von ihnen ist "Vernunft" wie bei dem lateinischen Wort ratio, von dem die Bezeichnung "rationale Zahlen" stammt. (Über logos ließe sich noch manches mehr berichten; das könnte in der diesem Artikel evtl. folgenden Diskussion geschehen.)
Die Definition des Begriffs "Logarithmus" wirkt ein wenig kompliziert, und nicht jeder hat sie parat. Meinen Schülern empfahl ich, sich als Einstieg zu merken: Logarithmen sind Hochzahlen, d. h. Exponenten bei der Potenzrechnung.
Am besten verdeutlicht man das anhand einiger einfacher Beispiele. So ist 23=8, 54=625, 106=1000000. Man sagt: "Die 3 ist der Logarithmus von 8 zur Basis 2" und schreibt 3=log28. Entsprechend gilt 4=log5625 und 6=log101000000. Im letzten Fall wird anstelle von log10 die Abkürzung lg verwendet: lg1000000=6, und man nennt die Logarithmen zur Basis 10 dekadische, gewöhnliche oder Zehnerlogarithmen.
Ein Logarithmus gibt Auskunft auf die Frage: womit muß ich eine Zahl b (die Basis) potenzieren, um eine vorgegeben Zahl a zu erhalten? In Zeichen: bx=a; dabei ist x die gesuchte Zahl, und es ist x=logba.
Aus dem folgenden Beispiel ergibt sich eine grundlegende Rechenregel für Logarithmen: Es ist 23⋅24=27=8⋅16=128, so daß log28+log216=7 und wegen 27=128 auch log2128=log2(8⋅16)=7 ist. Somit gilt log28+log216=log2(8⋅16), und dies wird verallgemeinert zu logbx+logby=logb(x⋅y). 1)
Das aber bedeutet: sollen zwei (im allgemeinen mehrstellige) Zahlen miteinander multipliziert werden, so sucht man aus der Tafel ihre Logarithmen, addiert diese und erhält als Ergebnis den Logarithmus des gesuchten Produkts. Dieses muß man nur noch "entlogarithmieren"; man sagt: ich suche den zugehörigen "Numerus" auf (numerus heißt einfach "Zahl"), der am Rand der Logarithmentafel zu finden ist.
Da sich die Zehnerlogarithmen am platzsparendsten tabellieren lassen, waren die für sie gedruckten Tafeln für die Schule stark verbreitet. So findet man mit einer einfachen, vierstelligen dekadischen Logarithmentafel [2] im Internet für das Produkt 50,54⋅236,7 den angenäherten Wert 11960, während das schriftliche Rechnen den genauen 11962,818 ergibt.
Mit einiger Übung beim Aufschlagen der Logarithmen und Finden der Numeri ist die Zeitersparnis, besonders bei größeren Zahlen, gegenüber dem normalen schriftlichen Rechnen beträchtlich; siehe das obige Laplace-Zitat. Die Astronomen benutzten zehn- und mehrstellige Logarithmentafeln, die ganze Bücherregale füllten.
Dividieren kann man ebenfalls mit Hilfe von Logarithmen, wobei logb(x/y)=logbx-logby ist, und auch potenzieren: es gilt logb(xy) = y⋅logbx. (Nützlich zu wissen ist noch logb1=0 und daß die Logarithmen von Zahlen zwischen 0 und 1 negativ sind.)
Von Interesse mag nun sein, wie man Logarithmen im einzelnen berechnet. Keineswegs sind sie immer ganze Zahlen wie bei unseren einführenden Beispielen. Durch das erste wissen wir, daß log28=3 ist; was aber ergibt sich z. B. für log27?
Im Laufe der Geschichte gab es zahlreiche Möglichkeiten zur Berechnung von Logarithmen, vgl. z. B. [3]. Am leichtesten läßt sie sich mit unseren heutigen Mitteln erklären, wenn als Basis die Eulersche Zahl
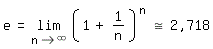
verwendet wird. Die dadurch entstehenden Logarithmen heißen "natürliche" und werden mit ln abgekürzt.
Sei f(x)=ln x, dann wird in der Analysis gelehrt, daß die Ableitungsfunktion f'(x)=1/x ist. Anmerkung: der Beweis dazu enthält einen nicht-trivialen Schritt, der bisweilen unerwähnt bleibt oder ohne (ausreichende) Begründung ausgeführt wird. Gemeint ist die Vertauschung von lim und ln, s. z. B. hier [4], [5]. Auch auf dem Matheplaneten spielte dies eine Rolle in [6], wobei mir scheint, daß die Sache im Sande verlief und nicht zu Ende diskutiert wurde.
Sei g(x)=ln(1+x), dann gilt entsprechend g'(x)=1/(1+x), und dies läßt sich als unendliche geometrische Reihe darstellen:
[ln(1+x)]'=1-x+x2-x3+-...
Integration auf beiden Seiten liefert
ln(1+x)=x-x2/2+x3/3-x4/4+-... (1)
plus eine Integrationskonstante, die sich für x=0 und wegen ln1=0 zu Null ergibt.
Diese Reihe konvergiert für -1<x≤1 und wird in [1] als Möglichkeit zur Berechnung natürlicher Logarithmen angegeben. Die Konvergenz wird umso schlechter, je mehr sich x den Intervallgrenzen nähert, und so taugt die Reihe nicht einmal zu einer befriedigenden, angenäherten Berechnung von ln2. Um auch nur wenige Nachkommastellen zu erhalten, muß man sehr viele Reihenglieder berücksichtigen.
Besser ist folgendes. Es gilt
[ln(1-x)]'=-1/(1-x)=-(1+x+x2+x3+...),
woraus durch Integration folgt:
ln(1-x)=-x-x2/2-x3/3-x4/4-... (2)
Zieht man (2) von (1) ab, entsteht
ln(1+x)-ln(1-x)=ln[(1+x)/(1-x)]=2(x+x3/3+x5/5+...) (3)
Wird hier (1+x)/(1-x)=2 gesetzt, was auf x=1/3 führt, erhält man
ln2=2(1/3+1/81+1/1215+1/15309+1/177147+1/1948617+...).
Mit den sechs angeschriebenen Summanden ergibt sich ln2≈0,693147; diesen Wert liefert, auf sechs Nachkommastellen gerundet, auch der Taschenrechner.
Nun muß man nicht so mit ln4 fortfahren, indem (1+x)/(1-x)=4 gesetzt und die entsprechende Reihe aufgestellt wird, sondern erhält viel einfacher ln4=2⋅ln2. Im Grunde genommen braucht man nacheinander nur die Logarithmen von Primzahlen zu berechnen; dann ergeben sich mit ihnen und den Logarithmen schon vorher berechneter Zahlen viele neue Logarithmen.
Setzen wir, um angenähert ln3 zu erhalten, in (3) (1+x)/(1-x)=3, entsteht mit x=1/2 die Reihe
ln3=2(1/2+1/24+1/160+1/896+...)=1+1/12+1/80+1/448+...
und entsprechend mit (1+x)/(1-x)=5, d. h. x=2/3, die Reihe
ln5=2(2/3+8/81+32/1215+...).
Die Reihe für ln3 konvergiert langsamer als die Reihe für ln2. Um dieselbe Genauigkeit wie dort (sechs Nachkommastellen) zu erhalten, benötigen wir bereits neun statt sechs Reihenglieder, und das verstärkt sich bei ln5 (15 Glieder), ln7 (21 Glieder) und allen weiteren Primzahlen, ist also auf die Dauer kein gangbarer Weg.
Als praktisch erweist sich dagegen Folgendes: sei p eine Primzahl, dann gilt
ln(p)-ln(p-1)=ln(p/(p-1)), und wenn wir das gleich
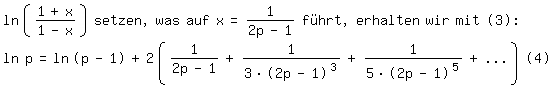
Damit und unter Verwendung des obigen Näherungswertes für ln 2 ergibt sich, auf sechs Stellen nach dem Komma gerundet
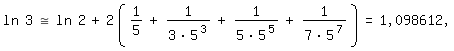
wozu nur die vier angeschriebenen Reihenglieder statt vorher neun nötig sind.
Die Darstellung (4) konvergiert, im Gegensatz zu (3), umso schneller, d. h., man benötigt bei vorgegebener Genauigkeit von ln p umso weniger Reihenglieder, je größer p ist. Mit (4) berechnet man sukzessive ln5, ln7, ln11 usw. und mit Hilfe der oben angegebenen Regeln auch Logarithmen wie ln2,401 = ln (74/1000) = 4ln7-3(ln2+ln5) oder ln(½⋅√3) = ln(3½/2) = ½⋅ln3-ln2.
Die natürlichen Logarithmen lassen sich gemäß
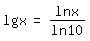
in dekadische umwandeln. Wie das zustandekommt, mögen diejenigen, die es interessiert, selber herausfinden.
Für das Rechnen mit Logarithmen ohne Papier und Bleistift wurden im Laufe der Zeit zahlreiche mechanische Geräte erfunden. Eine Übersicht mit Erklärungen findet man u. a. in [7]. Am bekanntesten wurde der Rechenschieber. Ein "virtueller", mit dem man selber experimentieren kann, läßt sich bei [8] bewundern.
-------------------
1) Es gilt also (wenn man der Bequemlichkeit halber die Basisbezeichnung b wegläßt): log(x⋅y)=log(x)+log(y)
und somit nicht log(x+y)=log(x)+log(y), was ein öfter vorkommender Anfängerfehler ist. Vielmehr ergibt sich:
log(x+y)=log(x)+log(y)+log(1/x+1/y), vgl. hier, Kommentar vom 7.8.2014,14:40:49.
[1] http://de.wikipedia.org/wiki/Logarithmus
[2] Logarithmentafel lg1000-lg2009 mit weiteren Seiten; man beachte den Hinweis zur fehlenden Interpolationsmöglichkeit.
[3] Abschnitt "Die Geschichte der Logarithmen,..." mit weiterführenden Links, insbesondere zu Napier (1550 bis 1617), einem der Pioniere auf dem Gebiet der Logarithmen
[4] Ableitung der Logarithmusfunktion
[5] Die Ableitungsfunktion der Logarithmus-Funktion ("hier darf ln und lim vertauscht werden")
[6] lim und ln vertauschen
[7] Rechenschieber, Walzen und Scheiben
[8] Interaktiver Rechenschieber
Zurück zur Themenübersicht, Teil 2