Ein junger Mathematikstudent verliebte sich in eine Kommilitonin, war aber zu schüchtern,
ihr das zu sagen. Um es wenigstens anzudeuten, schickte er ihr eine Geburtstagskarte,
die mit den folgenden Zeilen endete:
x = ±(-t² + 40t +1200) sin(πt/180)
y = (-t² + 40t + 1200) cos(πt/180), 0 ≤ t ≤ 60.
Diese Parameterdarstellung zeichnete sie mit ihrem Computer und erhielt
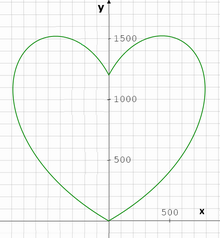 .
.
Die Geschichte ist nur ausgedacht, kann aber durchaus passieren, denn es gibt
viele Möglichkeiten, herzförmige Kurven durch mathematische Formeln darzustellen, vgl. hier [1].
Diese einfache Darstellung in Polarkoordinaten
r = π - |t| mit -π ≤ t ≤ π
ergibt nach Drehung um 90° nach rechts das Herz
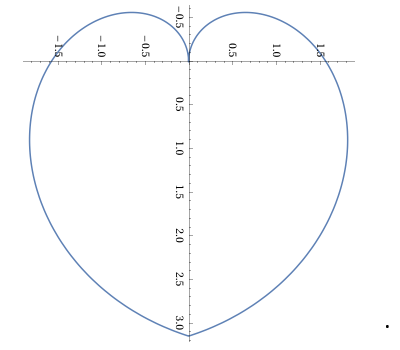
Mit einem kleinen Zusatz bekommt es eine Spitze:
r = π - |t| - 0.5 √|t| , -0.75 π ≤ t ≤ 0.75 π
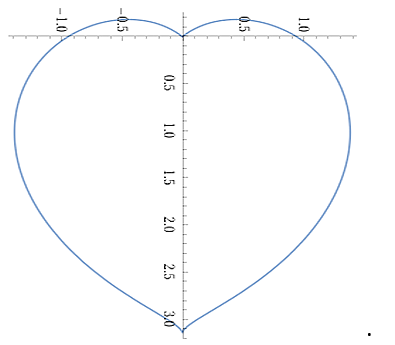
Die sogenannte "Herzkurve von Beutel"
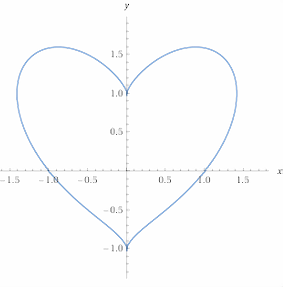
mit der Gleichung
(x² + y² -1)³ = 4x² y³
ist in [2] zu sehen. Sie steht dort auf dem Kopf, weil die +y-Achse, was ungewöhnlich ist,
nach unten geht.
Anschaulich-zielgerichtet leitet Peter Teuchert die Gleichung der Beutel-Herzkurve
hier her.
(Statt der 4 steht bei ihm der Faktor 1.)

[1] http//:www.mathematische-basteleien.de/herz.htm
[2] https://dbc.wroc.pl/Content/1673/PDF/001457.pdf, S. 145
[3] Lutherrose in manchen Kirchenfenstern. Rechts: an der Außenwand der Marktkirche in Halle
[4] http://matheplanet.com/matheplanet/nuke/html/article.php?sid=1272
Zurück zu Ausgewählte mathematische Kurven
Zurück zur Themenübersicht, Teil 2