Wie schon an anderer Stelle erwähnt, gibt es auf dem Matheplaneten in einer besonderen Rubrik auch mathematische Rätsel - oftmals sind das anspruchsvolle Aufgaben. Rebecca, Schülerin und hochgeschätztes Mitglied des Matheplaneten, stellte die folgende hier im Januar 2007:
"Gegeben sind zwei sich schneidende Geraden a und b sowie ein Punkt Q, der nicht auf diesen Geraden liegt. Der Schnittpunkt S der beiden Geraden liegt außerhalb des Zeichenpapiers. Man konstruiere lediglich mit einem unmarkierten Lineal die Gerade, auf der Q und S liegen."
Wenn nur ein unmarkiertes Lineal erlaubt ist, kann man nicht viel machen: es lassen sich Strecken ziehen (als Teile von gedachten Geraden) und die dabei entstehenden Schnittpunkte beobachten und interpretieren. Dies tat ich mit der folgenden Abbildung, deren Zustandekommen anschließend erklärt wird:
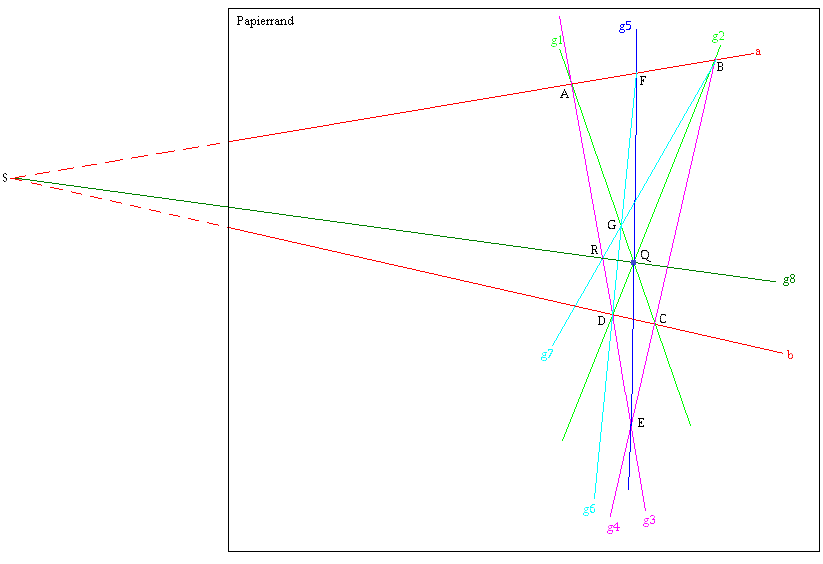
Als erstes zeichnete ich die beiden Geraden a und b und deutete gestrichelt an, wo sie sich außerhalb des Papierblattes in S schneiden. Dann wählte ich zwischen ihnen willkürlich den dunkelblau markierten Punkt Q. Durch ihn zeichnete ich die beiden grünen Geraden g1 und g2, die a und b in den Punkten A, B, C, D schneiden. Die beiden pinkfarbenen Geraden AD=g3 und BC=g4 schneiden sich im Punkt E. Von ihm aus geht durch Q die blaue Gerade g5, die a in F scheidet. Von F aus geht die Gerade g6 durch D. Sie schneidet g1 in G. Von B aus geht durch G die Gerade g7; sie schneidet g3 im Punkt R.
Von Q aus gesehen, liegt R in Richtung von S. Wird die durch Q und R gehende dunkelgrüne Gerade g8 eingezeichnet, so zeigt sich, daß sie die gesuchte ist.
Während in der ursprünglichen Aufgabenstellung nur die Konstruktion der Gerade durch Q, R und S gefordert wurde, hieß es später, sie solle auch noch anhand eines bekannten mathematischen Satzes begründet werden. Da meine obige Vorgehensweise rein intuitiv war, ohne theoretischen Hintergrund, hatte ich die Aufgabe erst zum Teil gelöst.
Welcher Satz anzuwenden sei, teilte Rebecca nicht mit, doch verwies sie auf eine Serie von insgesamt vier Artikeln auf dem Matheplaneten, in denen Florian Modler eine größere Anzahl von Sätzen über Dreiecke vorstellt und ausführlich erklärt. Den letzten Artikel mit Verweisen auf die drei vorangegehenden findet man hier.
Von den beschriebenen Sätzen kommt für unseren Zweck der Satz von Desargues in Betracht. Auf ihn bezieht sich die folgende Figur:
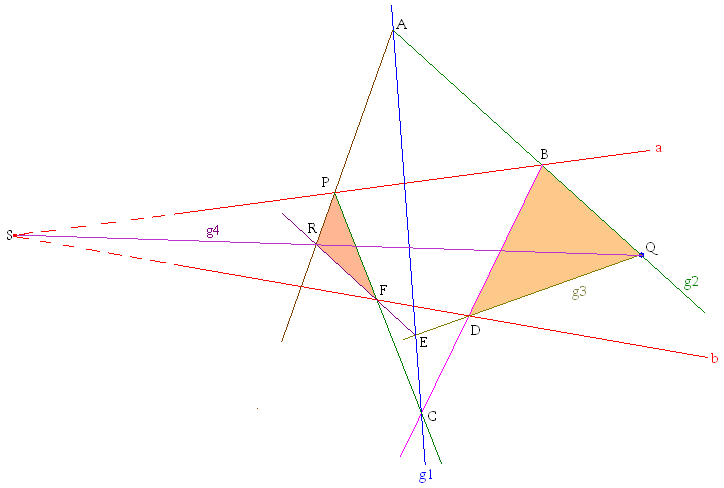
Nachdem die Geraden a und b und der Punkt Q gewählt wurden, wird eine beliebige Gerade g1 durch a und b gezogen. Auf ihr wird beliebig der Punkt A gewählt und mit Q verbunden. Der Schnittpunkt von AQ mit a heißt B. Er wird mit einem beliebigen Punkt C auf g1 verbunden. Die Gerade BC schneidet b im Punkt D. Q wird mit D verbunden und die Verbindungsstrecke so verlängert, daß sie g1 in E schneidet.
Dann wird auf a ein Punkt P frei gewählt und mit C verbunden. Die Gerade PC schneidet b im Punkt F. Schließlich wird noch die Gerade EF gezogen, die die Gerade AP im Punkt R schneidet.
Wir haben nun die beiden bräunlich gefärbten Dreiecke und insgesamt eine Figur zum Satz von Desargues.
Dieser besagt hier:
Wenn sich die Verbindungsgeraden RP und BQ, RF und DQ sowie PF und BD der Eckpunkte der beiden Dreiecke jeweils schneiden und die Schnittpunkte auf der Geraden AC liegen (was alles der Fall ist), dann liegen die Punkte Q, R und S auf einer Geraden.
Die durch Q und R gehende Gerade ist also die gesuchte.
Zurück zur Themenübersicht, Teil 2