Rätsel
Die neue Jahreszahl 2013 soll als Summe von drei Quadratzahlen geschrieben werden –
ohne Zuhilfenahme des Computers.
Lösung:
Mit den natürlichen Zahlen a,b,c soll gelten: 2013 = a² + b² + c². Da 2013 ungerade ist, müssen entweder zwei der drei Zahlen gerade und eine ungerade sein, oder alle drei sind ungerade.
Bei dieser letzten Möglichkeit erhält man mit a=2k+1, b=2l+1, c=2m+1: 2013=4(k²+l²+m²+k+l+m)+3, 1005=2(k²+l²+m²+k+l+m). Links steht eine ungerade, rechts eine gerade Zahl; also scheidet die Möglichkeit, daß alle drei Zahlen a,b,c ungerade sind, aus. Ich setze deshalb an: a=2k, b=2l, c=2m+1.
Dann gilt 2013 = 4k² + 4l² + 4m² + 4m +1 und weiter 2012 = 4 (k² + l² + m² + m), somit auch 503 = k² + l² + m² + m.
k und m sind so zu bestimmen, daß l² = 503 - k² - m² - m eine Quadratzahl ergibt.
Da a gerade sein soll, wähle ich als kleinste Möglichkeit a=2. Dann ist nach Obigem k=a/2=1,
so daß weiter folgt: l² = 503 - 1 – m² - m , l² = 502 - m² - m.
l² muß nicht nach der letzten Gleichung berechnet werden, indem man jedesmal m quadriert und dann zusammen mit m von 502 subtrahiert; es geht einfacher.
Für m=1 ist l²=502-1-1=500. Für m=2 ist l²=502-6=496; die Differenz zum Vorwert ist 4. Für m=3 ist l²=502-12=490; die Differenz zum Vorwert ist 6 usw. Diese Zahlen sind am Anfang der folgenden Tabelle eingetragen. Sie läßt sich sehr leicht zu Ende ausfüllen, da die Differenzen in der untersten Zeile das Doppelte der Zahlen in der obersten sind und man im Wesentlichen nur subtrahieren muß:

Die Tabelle endet mit der Quadratzahl l² = 196, d.h. es ist l = 14, woraus b =2 l = 28 und wegen m =17
c = 2m+1 = 35 folgt. Da wir a = 2 vorausgesetzt hatten, ist eine Lösung des Rätsels:
2013 = 2² + 28² + 35². Nach demselben Schema erhält man Lösungen für a=4 und a=8:
2013 = 4² + 34² + 29².
2013 = 8² + 10² + 43² .
Mit a=10 weiterzumachen, lohnt sich nicht. Man kann ja die letzte Lösung so umschreiben: 2013=10²+8²+43² und erhält dasselbe Ergebnis wie dort mit vertauschter Reihenfolge.
Die nächsten geraden Zahlen a=12 bis a=18 liefern, wie a=6, keine Lösung. Daß mit a=14 und a=16 die Bedingung a²+b²+c²=2013 nicht erfüllbar ist, habe ich wie oben durch Probieren gefunden. Bei 6, 12 und 18 ist das nicht nötig, und man spart Schreibarbeit. Die drei Zahlen sind durch 3 teilbar, und getrennt von dieser Seite habe ich festgestellt , daß die besagte Bedingung nur zu erfüllen ist, wenn keine der Zahlen a,b,c durch 3 teilbar ist.
Mit a=20 ergibt sich (wegen k=10) l²=403-m²-m und diese Tabelle:
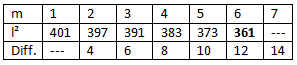
Aus m=6 ⇒ c=13, l²=361 ⇔ l=19 ⇒ b=38 sowie a=20 folgt:
2013 = 20² + 38² + 13².
Meine Lösung ist mathematisch wenig anspruchsvoll. Auf dem Matheplaneten wird hier ab Beitrag No. 13. stärker mit Abschätzungen und Fallunterscheidungen argumentiert.
Nachtrag:
Sehr einfach findet man mit dem Taschenrechner wegen 2013<45² zum Beispiel 2013 = 44² + 77 sowie 2013 = 43² + 164 = 43² + 100 + 64 = 43² + 10² + 8², unser vorletztes Ergebnis. Ebenso durch schrittweises Heruntergehen: 42,41,40,... bis 35: 35² - 2013 = -788 , 2013 = 35² + 788 = 35² + 784 + 4 = 35² + 28² + 2² wie oben und so weiter bis 29. Wie man feststellen kann, dass es nicht mehr als als die gefundenen vier Lösungen gibt, ist kompliziert und aufwendig. Erklärt (mit zahlreichen Fehlern) wird es
hier.
Zurück zur Rätselauswahl 2013
Zurück zur Themenübersicht