Sechs besondere Punkte auf den Seiten eines Dreiecks

Altbekannt ist und unzählige Male wiederholt wurde, dass sich die Seitenhalbierenden eines Dreiecks in dessen Schwerpunkt schneiden. Was aber passiert, wenn man die Seitenhälften nochmals halbiert? Welche Bedeutung haben die dabei entstehenden zusätzlichen Teilungspunkte der Dreiecksseiten?

Dieses Bild

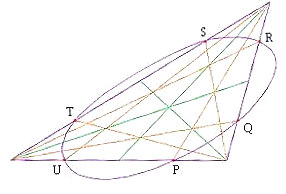
zeigt: Werden die Seiten eines beliebig schiefwinkligen Dreiecks halbiert, so liegen die Mittelpunkte der entstehenden Seitenhälften auf einer ellipsenähnlichen Kurve.

Die Kurve wurde freihändig skizziert; die sechs Punkte, durch die sie geht, sind:
P(15;0), Q(21;4), R(23,12), S(18;12), T(6;4) und U(5;0).

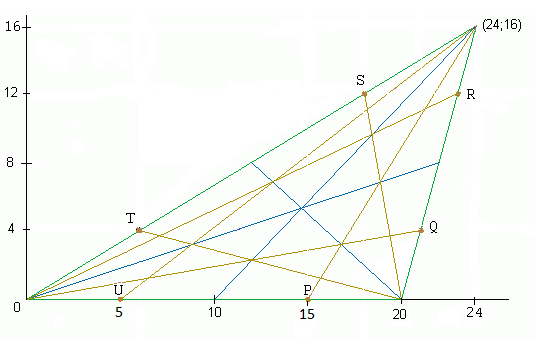
Um zu prüfen, ob es sich bei ihr um eine Ellipse oder nur eine dieser ähnliche Kurve handelt, setze ich die Koordinaten von P bis U in die Gleichung Ax²+By²+Cxy+Dx+Ey+F=0 für einen Kegelschnitt in allgemeiner Lage ein. So entsteht ein lineares Gleichungssystem aus sechs Gleichungen, von denen die ersten zwei lauten:
225A+ 0B+ 0C+15D+0E+F=0
441A+16B+84C+21D+4E+F=0.

Trivial ist die Lösung, bei der alle Koeffizienten A bis F gleich Null sind. Mit ihr ergibt sich keine Kurve. Um eine andere Lösung zu erhalten, bei der mindestens ein Koeffizient ungleich Null ist, setze ich A≠0 voraus. Dann entsteht nach beidseitiger Division aller Gleichungen durch A mit B'=B/A, C'=C/A usw. das System
  0B'+  0C'+15D'+ 0E'+F'=-225
 16B'+ 84C'+21D'+ 4E'+F'=-441
144B'+276C'+23D'+12E'+F'=-529
144B'+216C'+18D'+12E'+F'=-324
 16B'+ 24C'+ 6D'+ 4E'+F'=-36.

Seine Lösung lautet: B'=31/16, C'=-7/4, D'=-20, E'=5, F'=75. Durch Einsetzen in die veränderte Kegelschnittgleichung x²+B'y²+C'xy+D'x+E'y+F'=0 und anschließende beiderseitige Multiplikation mit dem Hauptnenner 16 ergibt sich die Gleichung
16x²+31y²-28xy-320x+80y+1200=0.   (1)

Ihr Graph ist, wie oben für möglich gehalten, eine Ellipse:


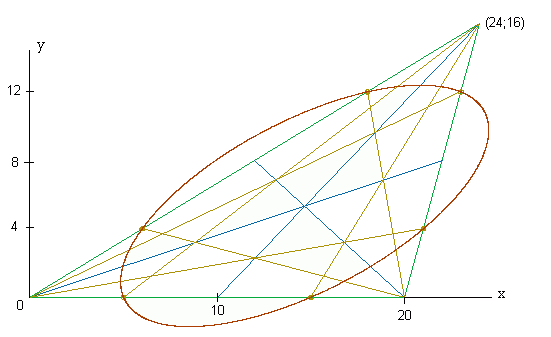
Auf die Hauptachsentransformation, um die einfachere Form x²/a²+y²/b²=1 mit den Halbachsen a,b zu erhalten, wird hier verzichtet. Sie ist rechnerisch sehr aufwendig und wird für das Folgende nicht benötigt.

An dieser Abbildung zeigt sich:

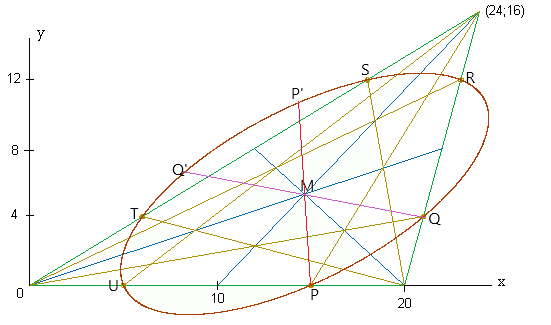
Die Strecken PM und MP', QM und MQ' sind jeweils gleich lang; Entsprechendes gilt für die vier übrigen Ellipsenpunkte R bis U.

Das bedeutet:
Möchte man für ein beliebig vorgegebenes Dreieck ohne Computer (der zum Zeichnen der Ellipse gebraucht wurde) und nur mit Zirkel und Lineal herausfinden, wie dessen zugehörige Ellipse ungefähr aussieht, kann man die sechs Mittelpunkte der Seitenhälften am Schwerpunkt des Dreiecks spiegeln, der zugleich der Mittelpunkt der Ellipse ist:



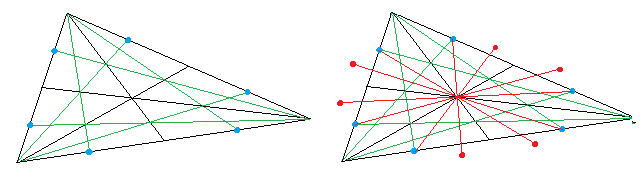
Auf diese einfache Weise ergeben sich zwölf Ellipsenpunkte, die sich durch unterschiedlich gekrümmte Bogenstücke von Hand miteinander verbinden lassen:



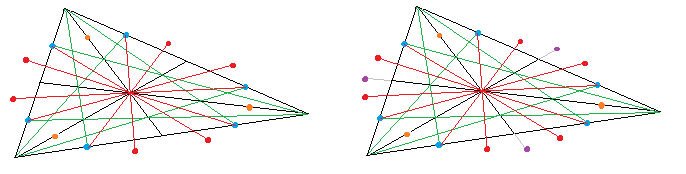
Das Vorstehende legt ohne allgemeinen, formalen Beweis den Satz nahe:

Die Mittelpunkte der Seitenhälften eines Dreiecks liegen auf einer Ellipse,
deren Mittelpunkt mit dem Schwerpunkt des Dreiecks übereinstimmt.

Der relativ breite Bereich zwischen P' und Q' enthält noch keinen, mit einfachen Konstruktionsschritten gefundenen Punkt.
Um ihn (und daraus folgende fünf weitere Punkte) geht es zum Abschluss.

In dieser Figur:



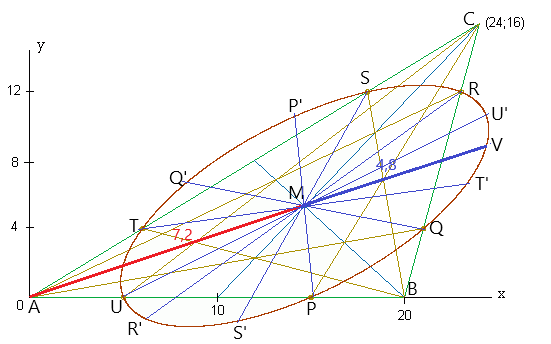
ist zusätzlich zu dem zuletzt erhaltenen Punkt U ein weiterer Punkt V markiert. Er entsteht dadurch, dass die rote Strecke AM um die blaue bis zur Ellipse verlängert wird. (Die eingetragenen Zahlen bedeuten die Längen in cm auf meinem Bildschirm.) Weil 7,2=3⋅2,4 und 4,8=2⋅2,4 ist, wird die Gesamtstrecke von A bis V durch den Mittelpunkt M im Verhältnis 3:2 geteilt. Um also den Punkt V zu erhalten, wird die rote Strecke dreigeteilt und eine der Teilstrecken verdoppelt; das ergibt dann die blaue.

Entsprechend erhält man zwei weitere Punkte W und X. Alle drei lassen sich an M spiegeln und ergeben V', W', X'.

Trägt man in die letzte Figur noch W,X,V',W',X' ein,


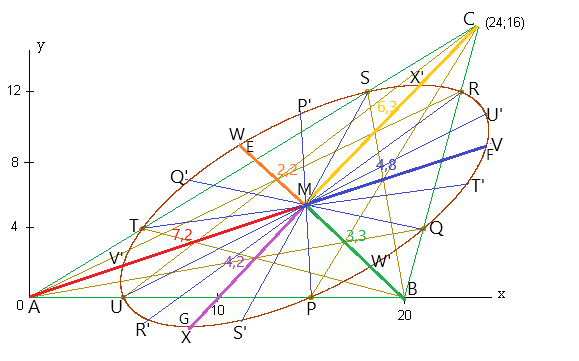
ergeben sich insgesamt 18 mit Zirkel und Lineal konstruierbare Ellipsenpunkte – das sind dreimal so viele wie am Anfang dieser Untersuchung.

Nachtrag
Die Annahme, dass der Mittelpunkt M die Strecken von den Ecken A, B, C bis zur Ellipse im Verhältnis 3:2 teilt, beruhte auf Anschauung und Messergebnissen, die kein wirklicher Beweis sind. Nach einem solchen suchte ich eine Zeit lang ohne Erfolg. Deshalb dachte ich, dass es ihn vielleicht gar nicht gibt. Zur Probe setzte ich die Koordinaten eines der letzten sechs konstruktiv erhalteten Punkte, des Punktes W, in die Gl.(1) ein und stellte fest, dass sie diese nicht erfüllen: statt der 0 auf der rechten Seite steht bei ihm ungefähr 14,8. Ähnliches ist bei den fünf übrigen Punkten zu erwarten. Das aber heißt: die Annahme mit der 3:2-Aufteilung ist falsch; dadurch liegt keiner der mit ihr erhaltenen Punkte auf der Ellipse. Die vorgestellte Dreiecks-Ellipsenkonstruktion liefert nur zwölf exakte Ellipsenpunkte.
Dennoch sind die letzten sechs konstruierten Punkte nicht nutzlos. Dies zeigt der Vergleich zwischen dem Punkt W mit den Koordinaten x_W=100/9=11,1; y_W=80/9=8,8 und dem angedeuteten wahren Ellipsenpunkt E. Ihn erhält man ohne die Annahme der Streckenaufteilung als Schnitt der Gerade durch B und M mit der Ellipse; dabei ergibt sich: x_E=(44-4√7)/3≈11,139; y_E≈8,861.
W und E sind eng benachbart, ebenso V und X mit den Ellipsenpunkten F und G. Das bedeutet: V,W,X und ihre Spiegelbilder liegen nicht genau, aber in guter Annäherung auf der Ellipse und können beim Skizzieren derselben von Hand wie die anderen zwölf Punkte verwendet werden. Damit ergibt sich die oben genannte Gesamtanzahl 18.

Zurück zur Themenübersicht, Teil 2